find ∫_0 ^π (dx/(cosx +sinx))


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 35059 by math khazana by abdo last updated on 14/May/18

$f i n d \int_{0}^{π} \frac{d x}{c o s x + s i n x}$
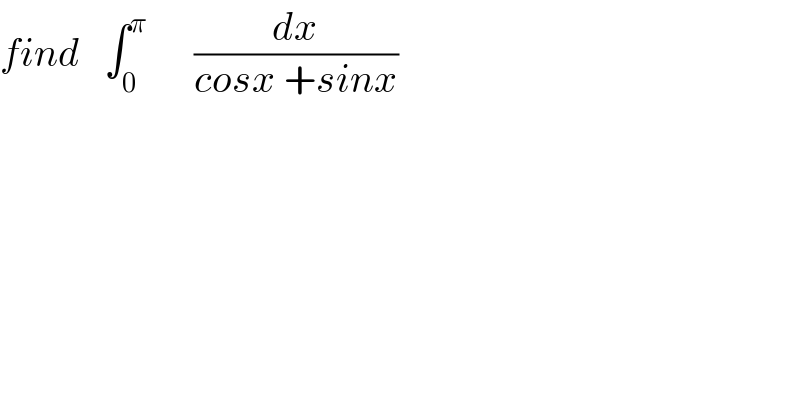
Commented by math khazana by abdo last updated on 15/May/18
$let put I = ∫_0 ^π (dx/(cosx +sinx)) changement tan((x/2))=t give x=2arctant and I = ∫_0 ^(+∞) (1/(((1−t^2 )/(1+t^2 )) +((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) I = ∫_0 ^(+∞) ((2dt)/(1−t^2 +2t)) = −2 ∫_0 ^∞ (dt/(t^2 −2t −1)) =−2 ∫_0 ^∞ (dt/((t−1)^2 −2)) =−2 ∫_0 ^∞ (dt/((t−3)(t+1))) =(1/2) ∫_0 ^∞ { (1/(t+1)) −(1/(t−3))}dt =(1/2) [ln∣((t+1)/(t−3))∣]_0 ^(+∞) =(1/2)( −ln((1/3))) I =(1/2)ln(3).$
$l e t p u t I = \int_{0}^{π} \frac{d x}{c o s x + s i n x} c h a n g e m e n t$ $t a n (\frac{x}{2}) = t g i v e x = 2 a r c t a n t a n d$ $I = \int_{0}^{+ \infty} \frac{1}{\frac{1 - t^{2}}{1 + t^{2}} + \frac{2 t}{1 + t^{2}}} \frac{2 d t}{1 + t^{2}}$ $I = \int_{0}^{+ \infty} \frac{2 d t}{1 - t^{2} + 2 t} = - 2 \int_{0}^{\infty} \frac{d t}{t^{2} - 2 t - 1}$ $= - 2 \int_{0}^{\infty} \frac{d t}{{(t - 1)}^{2} - 2}$ $= - 2 \int_{0}^{\infty} \frac{d t}{(t - 3) (t + 1)}$ $= \frac{1}{2} \int_{0}^{\infty} {\frac{1}{t + 1} - \frac{1}{t - 3}} d t$ $= \frac{1}{2} {[l n ∣ \frac{t + 1}{t - 3} ∣]}_{0}^{+ \infty} = \frac{1}{2} (- l n (\frac{1}{3}))$ $I = \frac{1}{2} l n (3) .$
Commented by prof Abdo imad last updated on 16/May/18
$error in the final lines I =−2 ∫_0 ^∞ (dt/((t−1)^2 −2)) =−2 ∫_0 ^∞ (dt/((t−1−_ (√2))(t−1 +(√2)))) =((−2)/(2(√2)))∫_0 ^∞ { (1/(t−1−(√2))) −(1/(t−1+(√2)))}dt =−(1/(√2))[ln∣((t−1−(√2))/(t−1+(√2)))]]_0 ^(+∞) =((−1)/(√2))( −ln(((1+(√2))/((√2) −1)))) I = (1/(√2))ln(((1+(√2))/(−1+(√2))))$
$e r r o r i n t h e f i n a l l i n e s$ $I = - 2 \int_{0}^{\infty} \frac{d t}{{(t - 1)}^{2} - 2}$ $= - 2 \int_{0}^{\infty} \frac{d t}{(t - 1 -_{} \sqrt{2}) (t - 1 + \sqrt{2})}$ $= \frac{- 2}{2 \sqrt{2}} \int_{0}^{\infty} {\frac{1}{t - 1 - \sqrt{2}} - \frac{1}{t - 1 + \sqrt{2}}} d t$ ${= - \frac{1}{\sqrt{2}} [l n ∣ \frac{t - 1 - \sqrt{2}}{t - 1 + \sqrt{2}}]]}_{0}^{+ \infty}$ $= \frac{- 1}{\sqrt{2}} (- l n (\frac{1 + \sqrt{2}}{\sqrt{2} - 1}))$ $I = \frac{1}{\sqrt{2}} l n (\frac{1 + \sqrt{2}}{- 1 + \sqrt{2}})$
	Answered by tanmay.chaudhury50@gmail.com last updated on 15/May/18

	$I = \int_{0}^{Π} \frac{d x}{c o s (Π - x) + s i n (Π - x)}$ $2 I = \int_{0}^{Π} \frac{1}{c o s x + s i n x} + \frac{1}{- c o s x + s i n x} d x$ $= \int_{0}^{Π} \frac{2 s i n x}{{s i n}^{2} x - {c o s}^{2} x} d x$ $I = \frac{1}{2} \int_{0}^{Π} \frac{2 s i n x}{1 - 2 {c o s}^{2} x} d x$ $= \int_{0}^{Π} \frac{(- s i n x)}{2 {c o s}^{2} x - 1} d x$ $= \frac{1}{2} \int_{0}^{Π} \frac{d (c o s x)}{{c o s}^{2} x - {(\frac{1}{\sqrt{2}})}^{2}}$ $= \frac{1}{2} \times \frac{\sqrt{2}}{2} ∣ l n \frac{c o s x - \frac{1}{\sqrt{2}}}{c o s x + \frac{1}{\sqrt{2}}} ∣_{0}^{Π}$
	Commented by NECx last updated on 15/May/18

	$p l e a s e h o w d i d y o u c h a n g e$ $\int_{0}^{π} \frac{1}{c o s x + s i n x} d x t o$ $\int_{0}^{π} \frac{1}{c o s (π - x) + s i n (π - x)} d x ? ? ?$
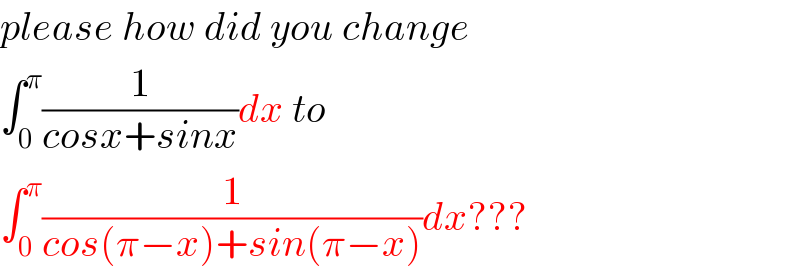
	Commented by tanmay.chaudhury50@gmail.com last updated on 15/May/18

	$\int_{0}^{a} f (x) d x = \int_{0}^{a} f (a - x) d x$
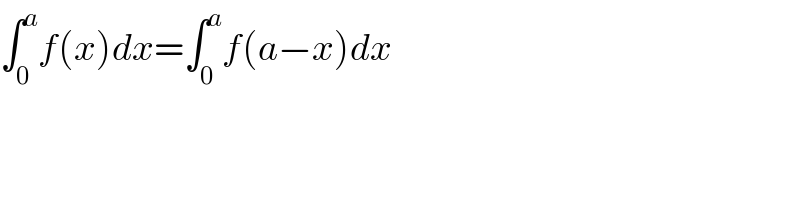
	Commented by NECx last updated on 15/May/18

	$o h . . . T h a n k s$
	Answered by tanmay.chaudhury50@gmail.com last updated on 15/May/18

	$\int \frac{d x}{c o s x + s i n x}$ $t = t a n \frac{x}{2} d t = \frac{1}{2} {s e c}^{2} \frac{x}{2}$ $\int \frac{d x}{\frac{1 - {t a n}^{2} \frac{x}{2}}{1 + {t a n}^{2} \frac{x}{2}} + \frac{2 t a n \frac{x}{2}}{1 + {t a n}^{2} \frac{x}{2}}}$ $\int \frac{{s e c}^{2} \frac{x}{2}}{1 - {t a n}^{2} \frac{x}{2} + 2 t a n \frac{x}{2}}$ $\int \frac{2 d t}{1 - t^{2} + 2 t}$ $- 2 \int \frac{d t}{t^{2} - 2 t + 1 - 2}$ $- 2 \int \frac{d t}{{(t - 1)}^{2} - {(\sqrt{2})}^{2}}$ $n o w u s e f o r m u l a a n d p u t l i m i t$ $o r m e t h o d$ $\int_{0}^{Π} \frac{d x}{c o s x + s i n x}$ $= \int_{0}^{Π} \frac{\frac{1}{\sqrt{2}} d x}{\frac{1}{\sqrt{2}} c o s x + \frac{1}{\sqrt{2}} s i n x}$ $= \frac{1}{\sqrt{2}} \int_{0}^{Π} \frac{d x}{s i n (Π / 4 + x)}$ $n o w u s e f o r m u l a a n d p u t l i m i t$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum