
Question and Answers Forum
Question Number 28885 by abdo imad last updated on 31/Jan/18
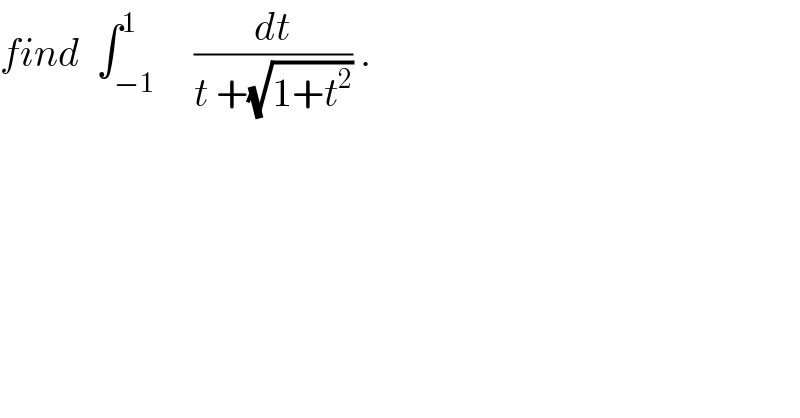
Commented by abdo imad last updated on 02/Feb/18
![let put I= ∫_(−1) ^1 (dt/(t +(√(1+t^2 )))) I= ∫_(−1) ^1 (((√(1+t^2 )) −t)/(1+t^2 −t^2 ))dt= ∫_(−1) ^1 (√(1+t^2 dt)) −∫_(−1) ^1 tdt = 2∫_0 ^1 (√(1+t^2 )) dt −0= 2 ∫_0 ^1 (√(1+t^2 )) dt the ch.t=tanx give ∫_0 ^1 (√(1+t^2 )) dt= ∫_0 ^(π/4) cosx (1+tan^2 x)dx= ∫_0 ^(π/4) (dx/(cosx)) and the ch. tan((x/2))=u give ∫_0 ^(π/4) (dx/(cosx))= ∫_0 ^((√2)−1) (1/((1−u^2 )/(1+u^2 ))) ((2du)/(1+u^2 ))=∫_0 ^((√2)−1) ((2du)/(1−u^2 )) =∫_0 ^((√2)−1) ( (1/(1+u)) +(1/(1−u)))du =[ln∣((1+u)/(1−u))∣]_0 ^((√2) −1) =ln( ((√2)/(2−(√2))))=ln( ((√2)/((√2)((√2)−1))))= −ln((√2)−1). I=−2ln((√2)−1).](Q28966.png)
| ||
Question and Answers Forum | ||
Question Number 28885 by abdo imad last updated on 31/Jan/18 | ||
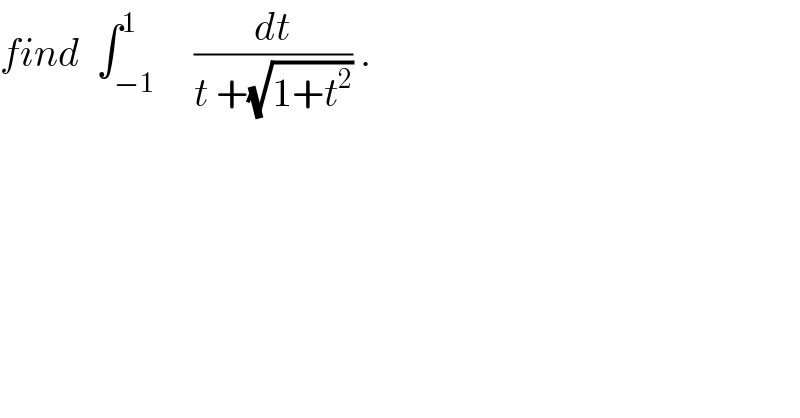 | ||
Commented by abdo imad last updated on 02/Feb/18 | ||
![let put I= ∫_(−1) ^1 (dt/(t +(√(1+t^2 )))) I= ∫_(−1) ^1 (((√(1+t^2 )) −t)/(1+t^2 −t^2 ))dt= ∫_(−1) ^1 (√(1+t^2 dt)) −∫_(−1) ^1 tdt = 2∫_0 ^1 (√(1+t^2 )) dt −0= 2 ∫_0 ^1 (√(1+t^2 )) dt the ch.t=tanx give ∫_0 ^1 (√(1+t^2 )) dt= ∫_0 ^(π/4) cosx (1+tan^2 x)dx= ∫_0 ^(π/4) (dx/(cosx)) and the ch. tan((x/2))=u give ∫_0 ^(π/4) (dx/(cosx))= ∫_0 ^((√2)−1) (1/((1−u^2 )/(1+u^2 ))) ((2du)/(1+u^2 ))=∫_0 ^((√2)−1) ((2du)/(1−u^2 )) =∫_0 ^((√2)−1) ( (1/(1+u)) +(1/(1−u)))du =[ln∣((1+u)/(1−u))∣]_0 ^((√2) −1) =ln( ((√2)/(2−(√2))))=ln( ((√2)/((√2)((√2)−1))))= −ln((√2)−1). I=−2ln((√2)−1).](Q28966.png) | ||