Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 64866 by mathmax by abdo last updated on 22/Jul/19

$$find{\int }_1^{+\mathrm{\infty }}\frac{dx}{x^2\sqrt{1+x+x^2}}$$

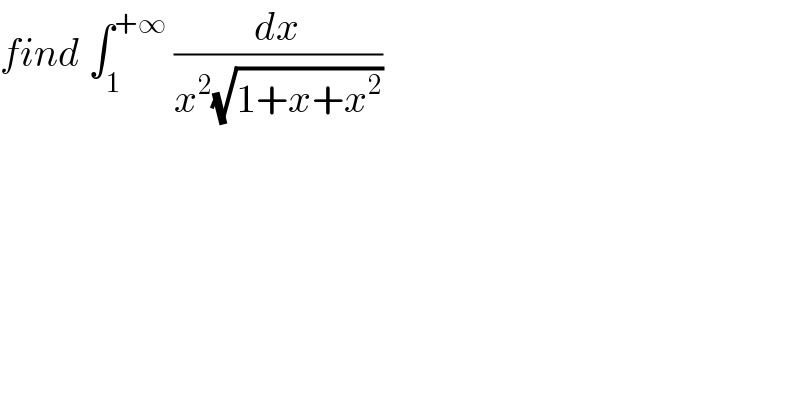
Commented by mathmax by abdo last updated on 23/Jul/19

$$letA={\int }_1^{+\mathrm{\infty }}\frac{dx}{x^2\sqrt{x^2+x+1}}wehave{x}^2+x+1={(x+\frac{1}{2})}^2+\frac{3}{4}$$$$changementx+\frac{1}{2}=\frac{\sqrt{3}}{2}sh\left(t\right)givesh\left(t\right)=\frac{2x+1}{\sqrt{3}}$$$$A={\int }_{argsh\left(\sqrt{3}\right)}^{+\mathrm{\infty }}\frac{1}{{(\frac{\sqrt{3}}{2}sht-\frac{1}{2})}^2\frac{\sqrt{3}}{2}ch\left(t\right)}\frac{\sqrt{3}}{2}ch\left(t\right)dt$$$$=4{\int }_{ln(\sqrt{3}+\sqrt{4})}^{+\mathrm{\infty }}\frac{dt}{{(\sqrt{3}sh\left(t\right)-1)}^2}=4{\int }_{ln(2+\sqrt{3})}^{+\mathrm{\infty }}\frac{dt}{3{sh}^{2}t-2\sqrt{3}sht+1}$$$$=4{\int }_{ln(2+\sqrt{3})}^{+\mathrm{\infty }}\frac{dt}{3\frac{ch\left(2t\right)-1}{2}-2\sqrt{3}sh\left(t\right)+1}$$$$=8{\int }_{ln(2+\sqrt{3})}^{+\mathrm{\infty }}\frac{dt}{3ch\left(2t\right)-3-4\sqrt{3}sh\left(t\right)+2}$$$$=8{\int }_{ln(2+\sqrt{3})}^{+\mathrm{\infty }}\frac{dt}{3ch\left(2t\right)-4\sqrt{3}sh\left(t\right)-1}$$$$=8{\int }_{ln(2+\sqrt{3})}^{+\mathrm{\infty }}\frac{dt}{3\frac{e^{2t}+e^{-2t}}{2}-4\sqrt{3}\frac{e^t-e^{-t}}{2}-1}$$$$=16{\int }_{ln(2+\sqrt{3})}^{+\mathrm{\infty }}\frac{dt}{3e^{2t}+3e^{-2t}-4\sqrt{3}{e}^t+4\sqrt{3}{e}^{-t}-2}$$$${=}_{e^t=u}16{\int }_{2+\sqrt{3}}^{+\mathrm{\infty }}\frac{du}{u(3u^2+3u^{-2}-4\sqrt{3}u+4\sqrt{3}{u}^{-1}-2)}$$$$=16{\int }_{2+\sqrt{3}}^{+\mathrm{\infty }}\frac{du}{3u^3+3u^{-1}-4\sqrt{3}{u}^2+4\sqrt{3}-2u}$$$$=16{\int }_{2+\sqrt{3}}^{+\mathrm{\infty }}\frac{udu}{3u^4+3-4\sqrt{3}{u}^3+4\sqrt{3}u-2u^2}letdecompose$$$$F\left(u\right)=\frac{u}{3u^4-4\sqrt{3}{u}^3-2u^2+4\sqrt{3}u+3}....becontinued....$$$$$$

Commented by ~ À ® @ 237 ~ last updated on 25/Jul/19

$$letuschangeu=\frac{1}{x}du=-\frac{dx}{x^2}$$$$thenwehaveI={\int }_0^1\frac{udu}{\sqrt{1+u+u^2}}=\frac{1}{2}[{\int }_0^1\frac{2u+1}{\sqrt{1+u+u^2}}du-{\int }_0^1\frac{du}{\sqrt{1+u+u^2}}]$$$$forthe{2}^{nd}integralJweknowsthat1+u+u^2=\frac{3}{4}[{\left(\frac{2u+1}{\sqrt{3}}\right)}^2+1]$$$$letuschangev=arctan\left(\frac{2u+1}{\sqrt{3}}\right)dv=\frac{\frac{2}{\sqrt{3}}du}{{\left(\frac{2u+1}{\sqrt{3}}\right)}^2+1}$$$$so$$$$J={\int }_0^1\frac{du}{\sqrt{1+u+u^2}}={\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}\sqrt{{tan}^{2}v+1}dv={\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{dv}{cosv}={\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{cosvdv}{(1-sinv)(1+sinv)}={\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{1}{2}.[\frac{cosv}{1-sinv}+\frac{cosv}{1+sinv}]dv$$$$={[\frac{1}{2}ln\mid \frac{1+sinv}{1-sinv}\mid ]}_{\frac{\pi }{6}}^{\frac{\pi }{3}}=ln\left(\frac{4+2\sqrt{3}}{3}\right)$$$$Now$$$$I=\frac{1}{2}.({\left[2\sqrt{1+u+u^2}\right]}_0^1-J)=\frac{1}{2}.[(2\sqrt{3}-2)-ln\left(\frac{4+2\sqrt{3}}{3}\right)]$$$$$$

Commented by mathmax by abdo last updated on 28/Jul/19

$$thankyousir.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com