
Question and Answers Forum
Question Number 31503 by abdo imad last updated on 09/Mar/18
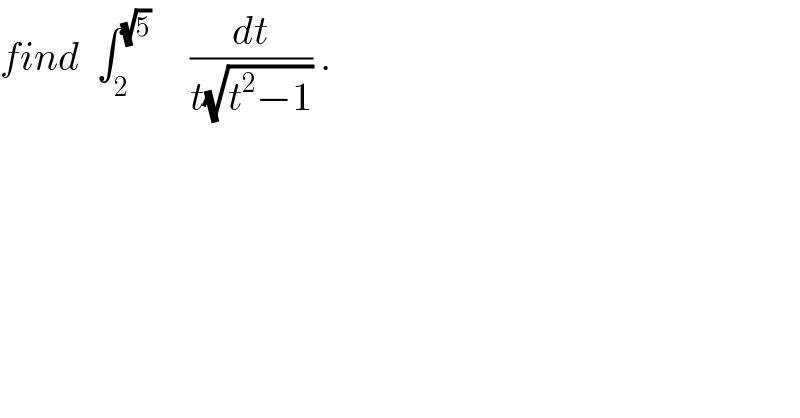
Commented by abdo imad last updated on 16/Mar/18
![ch. t=ch(x) give I = ∫_(argch(2)) ^(argch((√5))) ((shxdx)/(ch(x)sh(x))) = ∫_(argch(2)) ^(argch((√5))) (dx/((e^x +e^(−x) )/2)) = 2 ∫_(argch2)) ^(argch((√5))) (dx/(e^x +e^(−x) )) let use the ch. e^x =t ⇒ I = 2 ∫_e^(argch(2)) ^e^(argch((√5))) (dt/(t(t +(1/t)))) = 2 ∫_e^(argch(2)) ^e^(argch((√5) )) (dt/(t^2 +1)) = 2 [ arctan(t)]_e^(argch(2)) ^e^(argch((√5))) but we know that argch(x)=ln(x +(√( x^2 −1_ )))⇒ argch(2)=ln(2+(√3)) and argch((√5))=ln((√5) +2) I= 2[arctan(t)]_(2+(√3)) ^(2+(√5)) =2( arctan(2+(√5))−arctan(2+(√3)))](Q31912.png)
| ||
Question and Answers Forum | ||
Question Number 31503 by abdo imad last updated on 09/Mar/18 | ||
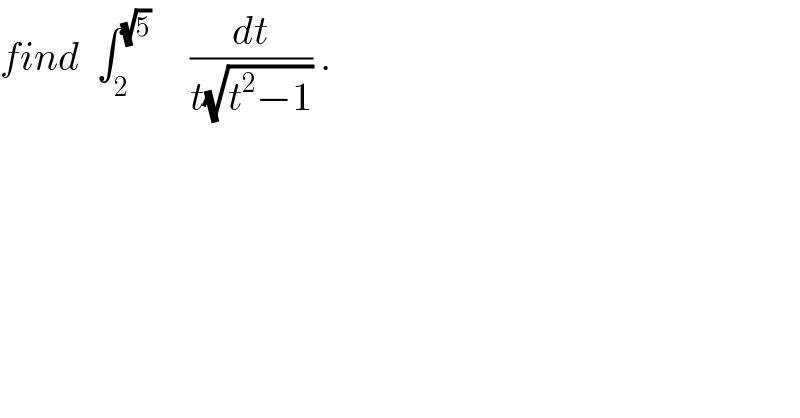 | ||
Commented by abdo imad last updated on 16/Mar/18 | ||
![ch. t=ch(x) give I = ∫_(argch(2)) ^(argch((√5))) ((shxdx)/(ch(x)sh(x))) = ∫_(argch(2)) ^(argch((√5))) (dx/((e^x +e^(−x) )/2)) = 2 ∫_(argch2)) ^(argch((√5))) (dx/(e^x +e^(−x) )) let use the ch. e^x =t ⇒ I = 2 ∫_e^(argch(2)) ^e^(argch((√5))) (dt/(t(t +(1/t)))) = 2 ∫_e^(argch(2)) ^e^(argch((√5) )) (dt/(t^2 +1)) = 2 [ arctan(t)]_e^(argch(2)) ^e^(argch((√5))) but we know that argch(x)=ln(x +(√( x^2 −1_ )))⇒ argch(2)=ln(2+(√3)) and argch((√5))=ln((√5) +2) I= 2[arctan(t)]_(2+(√3)) ^(2+(√5)) =2( arctan(2+(√5))−arctan(2+(√3)))](Q31912.png) | ||