
Question and Answers Forum
Question Number 60494 by Mr X pcx last updated on 21/May/19
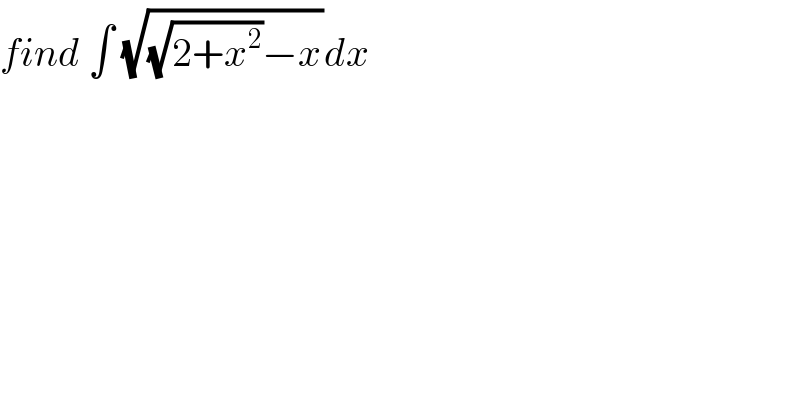
Commented by maxmathsup by imad last updated on 22/May/19
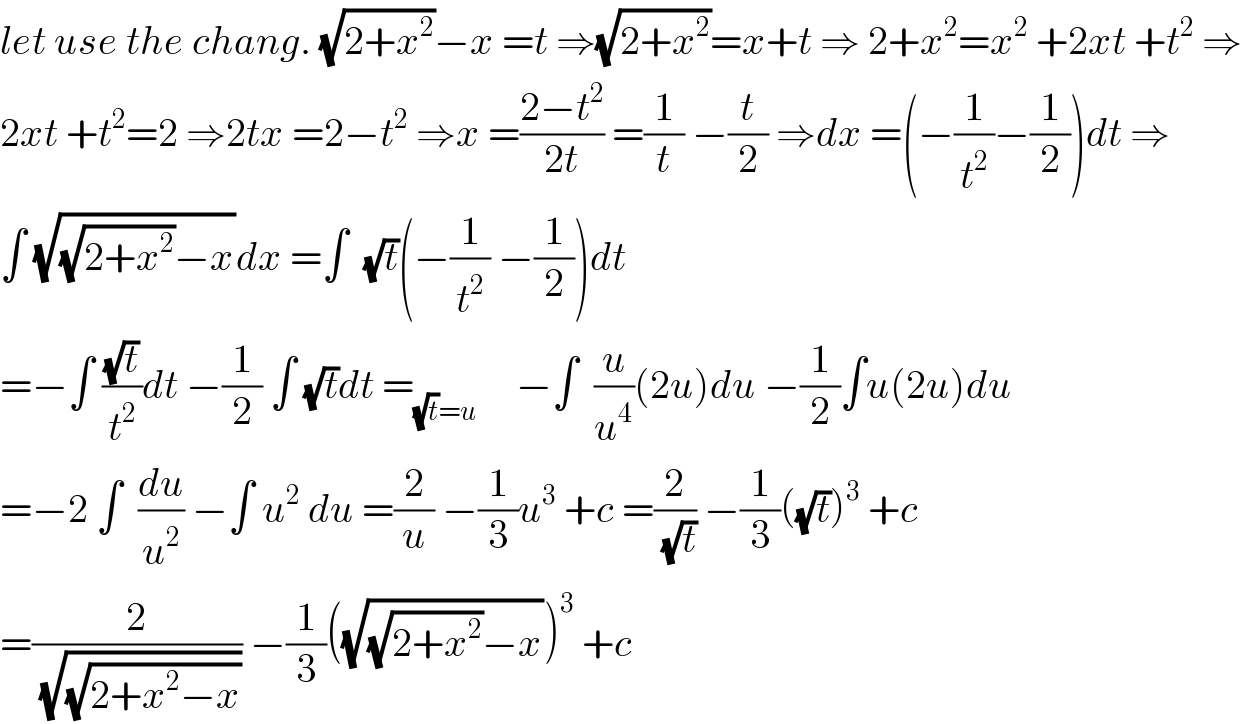
Answered by MJS last updated on 21/May/19
![∫(√((√(x^2 +2))−x))dx= [t=(√((√(x^2 +2))−x)) → dx=−((2(√(x^2 +2)))/(√((√(x^2 +2))−x)))dt] [⇒ x=((2−t^4 )/(2t^2 )) ⇒ dx=−((t^4 +2)/t^3 )dt] =−∫((t^4 +2)/t^2 )dt=−∫t^2 dt−2∫(dt/t^2 )=−(t^3 /3)+(2/t)= =((6−t^4 )/(3t))=(2/3)(x(√((√(x^2 +2))−x))+(2/(√((√(x^2 +2))−x))))+C](Q60528.png)
Commented by maxmathsup by imad last updated on 22/May/19

| ||
Question and Answers Forum | ||
Question Number 60494 by Mr X pcx last updated on 21/May/19 | ||
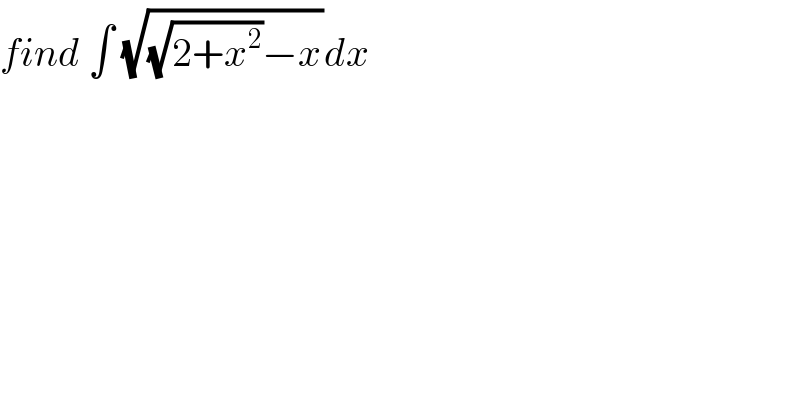 | ||
Commented by maxmathsup by imad last updated on 22/May/19 | ||
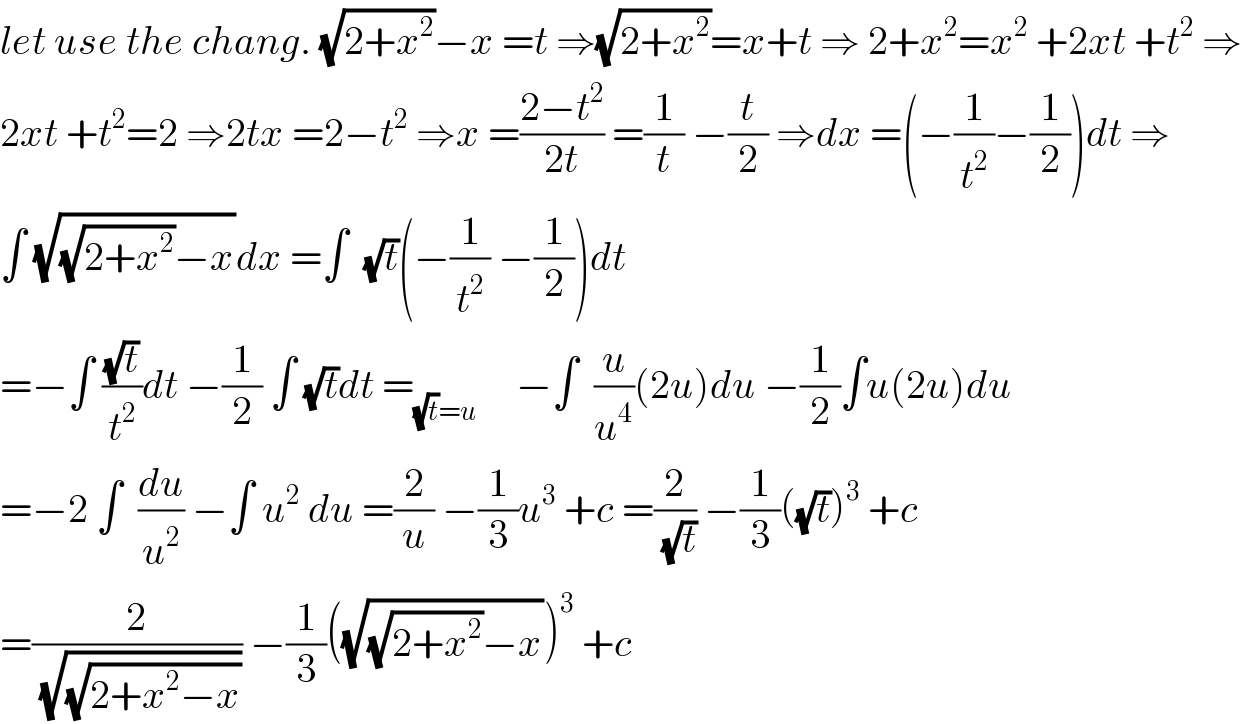 | ||
Answered by MJS last updated on 21/May/19 | ||
![∫(√((√(x^2 +2))−x))dx= [t=(√((√(x^2 +2))−x)) → dx=−((2(√(x^2 +2)))/(√((√(x^2 +2))−x)))dt] [⇒ x=((2−t^4 )/(2t^2 )) ⇒ dx=−((t^4 +2)/t^3 )dt] =−∫((t^4 +2)/t^2 )dt=−∫t^2 dt−2∫(dt/t^2 )=−(t^3 /3)+(2/t)= =((6−t^4 )/(3t))=(2/3)(x(√((√(x^2 +2))−x))+(2/(√((√(x^2 +2))−x))))+C](Q60528.png) | ||
| ||
Commented by maxmathsup by imad last updated on 22/May/19 | ||
 | ||