
Question and Answers Forum
Question Number 35677 by abdo imad last updated on 21/May/18
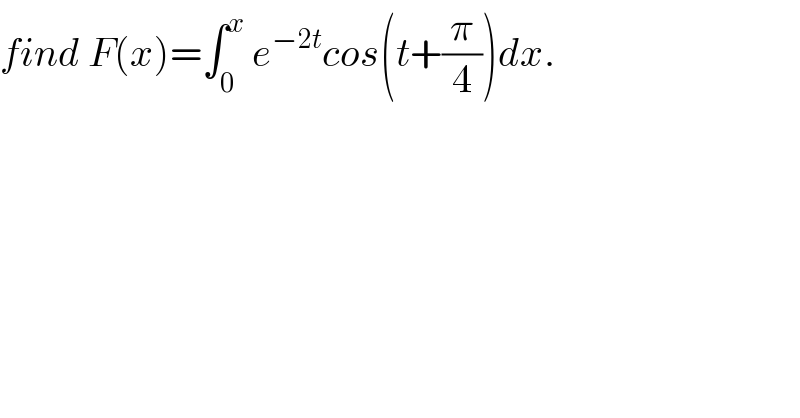
Commented by prof Abdo imad last updated on 23/May/18
![we have F(x)= Re( ∫_0 ^x e^(−2t) e^(i(t+(π/4))) dt) =Re( ∫_0 ^x e^(−2t +i(t +(π/4))) dt) but ∫_0 ^x e^(−2t +i(t+(π/4))) dt = ∫_0 ^x e^((−2+i)t +i(π/4)) dt =e^(i(π/4)) ∫_0 ^x e^((−2+i)t) dt = e^(i(π/4)) [(1/(−2+i)) e^((−2+i)t) ]_0 ^x = (e^(i(π/4)) /(−2+i)){ e^((−2+i)x) −1} = (((−2−i) e^(i(π/4)) )/5) e^(−2x) { cosx +isinx −1} =−(1/5){ (2+i)(((√2)/2) +i((√2)/2))}e^(−2x) { cosx +isinx −1} =−((2(√2))/5){ (2+i)(1+i)}e^(−2x) {cosx +isinx−1} =−((2(√2))/5)e^(−2x) ( 2 +2i +i−1){ cosx +isinx −1} =−((2(√2))/5)e^(−2x) ( 1+3i){ cosx +isinx −1} = −((2(√2))/5) e^(−2x) { cosx +isinx −1 +3i cosx −3sinx−3i} F(x)= −((2(√2))/5) e^(−2x) { cosx −3sinx −1} .](Q35800.png)
Commented by prof Abdo imad last updated on 23/May/18
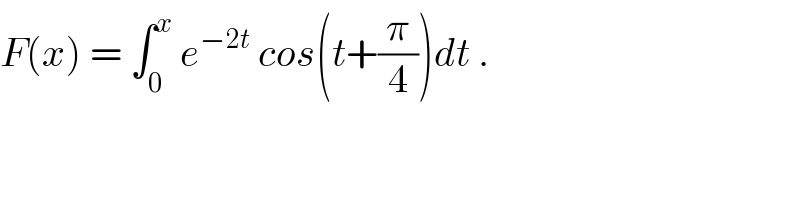
| ||
Question and Answers Forum | ||
Question Number 35677 by abdo imad last updated on 21/May/18 | ||
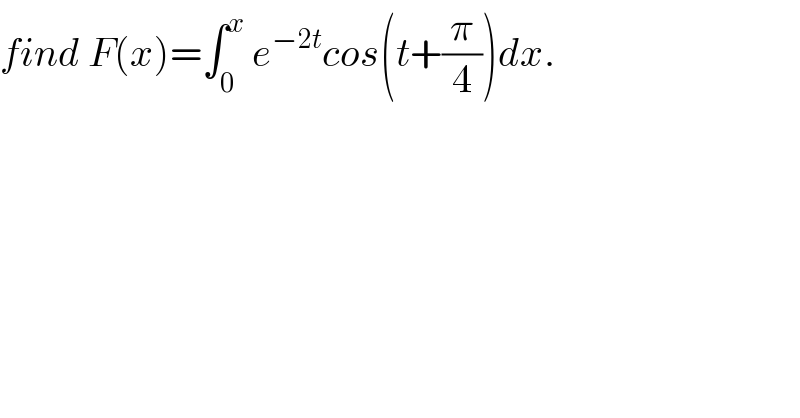 | ||
Commented by prof Abdo imad last updated on 23/May/18 | ||
![we have F(x)= Re( ∫_0 ^x e^(−2t) e^(i(t+(π/4))) dt) =Re( ∫_0 ^x e^(−2t +i(t +(π/4))) dt) but ∫_0 ^x e^(−2t +i(t+(π/4))) dt = ∫_0 ^x e^((−2+i)t +i(π/4)) dt =e^(i(π/4)) ∫_0 ^x e^((−2+i)t) dt = e^(i(π/4)) [(1/(−2+i)) e^((−2+i)t) ]_0 ^x = (e^(i(π/4)) /(−2+i)){ e^((−2+i)x) −1} = (((−2−i) e^(i(π/4)) )/5) e^(−2x) { cosx +isinx −1} =−(1/5){ (2+i)(((√2)/2) +i((√2)/2))}e^(−2x) { cosx +isinx −1} =−((2(√2))/5){ (2+i)(1+i)}e^(−2x) {cosx +isinx−1} =−((2(√2))/5)e^(−2x) ( 2 +2i +i−1){ cosx +isinx −1} =−((2(√2))/5)e^(−2x) ( 1+3i){ cosx +isinx −1} = −((2(√2))/5) e^(−2x) { cosx +isinx −1 +3i cosx −3sinx−3i} F(x)= −((2(√2))/5) e^(−2x) { cosx −3sinx −1} .](Q35800.png) | ||
Commented by prof Abdo imad last updated on 23/May/18 | ||
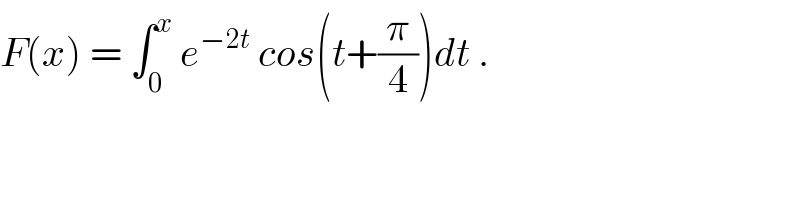 | ||