
Question and Answers Forum
Question Number 31073 by abdo imad last updated on 02/Mar/18
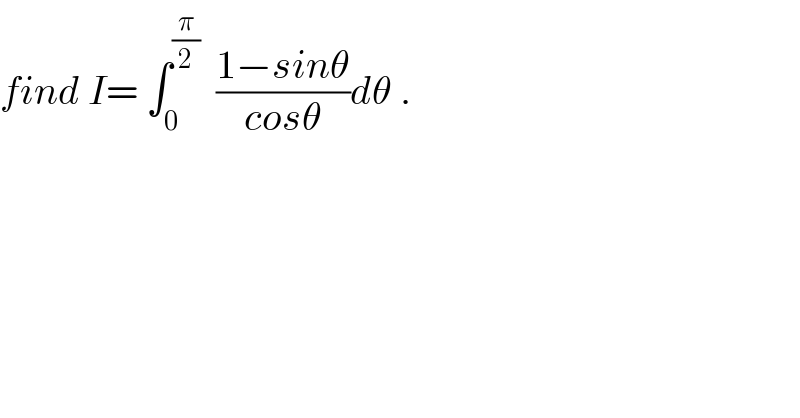
Commented by prof Abdo imad last updated on 03/Mar/18
![the ch.tan((θ/2))=x give I=∫_0 ^1 ((1 −((2x)/(1+x^2 )))/((1−x^2 )/(1+x^2 ))) ((2dx)/(1+x^2 )) = 2∫_0 ^1 (((x−1)^2 )/((1−x^2 )(1+x^2 )))dx =2 ∫_0 ^1 ((1−x)/((1+x)(1+x^2 )))dx let decompose the frsction F(x)= ((1−x)/((1+x)(1+x^2 ))) = (a/(1+x)) +((bx +c)/(1+x^2 )) a=lim_(x→−1) (x+1)F(x)= (2/2)=1 lim_(x→+∞) xF(x)= 0=a+b ⇒b=−a=−1 ⇒ F(x)= (1/(1+x)) +((−x+c)/(1+x^2 )) F(0)=1= 1+c⇒c=0 soF(x)= (1/(1+x)) −(x/(1+x^2 ))⇒ I= 2∫_0 ^1 (dx/(1+x))dx +∫_0 ^1 ((2x)/(1+x^2 ))dxp = 2[ln∣1+x∣]_0 ^(1 ) −[ln(1+x^2 )]_0 ^1 = 2ln(2) −ln(2)⇒ I=ln(2) .](Q31140.png)
Answered by Joel578 last updated on 02/Mar/18
![I = lim_(t→(π/2)) (∫_0 ^t sec x − tan x dx) = lim_(t→(π/2)) [ln (sec x + tan x)cos x]_0 ^t = lim_(t→(π/2)) ln ((sec t + tan t)cos t) − ln (1 + 0) = lim_(t→(π/2)) ln ((sec t + tan t)cos t) = lim_(t→(π/2)) ln (1 + tan t cos t) = ln (1 + lim_(t→(π/2)) tan t cos t) = ln (1 + lim_(t→(π/2)) ((cos t)/(cot t))) = ln (1 + lim_(t→(π/2)) ((−sin t)/(−cosec^2 t))) = ln 2](Q31134.png)
| ||
Question and Answers Forum | ||
Question Number 31073 by abdo imad last updated on 02/Mar/18 | ||
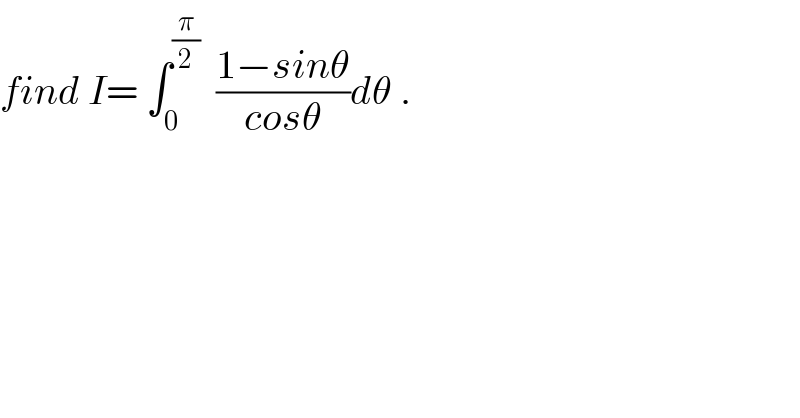 | ||
Commented by prof Abdo imad last updated on 03/Mar/18 | ||
![the ch.tan((θ/2))=x give I=∫_0 ^1 ((1 −((2x)/(1+x^2 )))/((1−x^2 )/(1+x^2 ))) ((2dx)/(1+x^2 )) = 2∫_0 ^1 (((x−1)^2 )/((1−x^2 )(1+x^2 )))dx =2 ∫_0 ^1 ((1−x)/((1+x)(1+x^2 )))dx let decompose the frsction F(x)= ((1−x)/((1+x)(1+x^2 ))) = (a/(1+x)) +((bx +c)/(1+x^2 )) a=lim_(x→−1) (x+1)F(x)= (2/2)=1 lim_(x→+∞) xF(x)= 0=a+b ⇒b=−a=−1 ⇒ F(x)= (1/(1+x)) +((−x+c)/(1+x^2 )) F(0)=1= 1+c⇒c=0 soF(x)= (1/(1+x)) −(x/(1+x^2 ))⇒ I= 2∫_0 ^1 (dx/(1+x))dx +∫_0 ^1 ((2x)/(1+x^2 ))dxp = 2[ln∣1+x∣]_0 ^(1 ) −[ln(1+x^2 )]_0 ^1 = 2ln(2) −ln(2)⇒ I=ln(2) .](Q31140.png) | ||
Answered by Joel578 last updated on 02/Mar/18 | ||
![I = lim_(t→(π/2)) (∫_0 ^t sec x − tan x dx) = lim_(t→(π/2)) [ln (sec x + tan x)cos x]_0 ^t = lim_(t→(π/2)) ln ((sec t + tan t)cos t) − ln (1 + 0) = lim_(t→(π/2)) ln ((sec t + tan t)cos t) = lim_(t→(π/2)) ln (1 + tan t cos t) = ln (1 + lim_(t→(π/2)) tan t cos t) = ln (1 + lim_(t→(π/2)) ((cos t)/(cot t))) = ln (1 + lim_(t→(π/2)) ((−sin t)/(−cosec^2 t))) = ln 2](Q31134.png) | ||
| ||