find I_n = ∫_0 ^1 x^n (√(1−x^2 ))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 42798 by maxmathsup by imad last updated on 02/Sep/18

$f i n d I_{n} = \int_{0}^{1} x^{n} \sqrt{1 - x^{2}} d x$
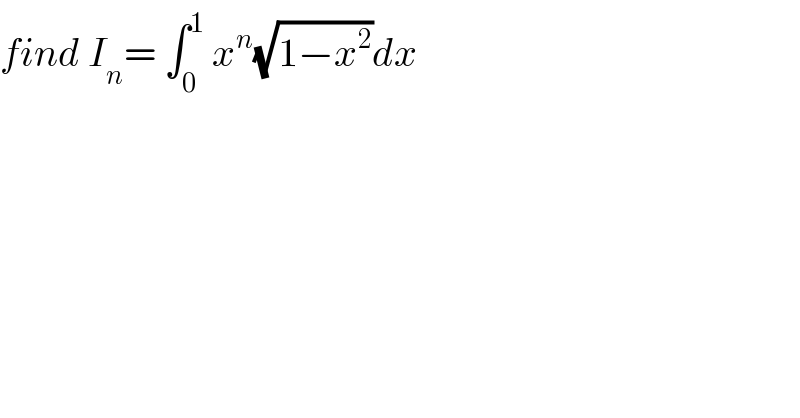
Commented by maxmathsup by imad last updated on 05/Sep/18
$changement x=sint give I_n = ∫_0 ^(π/2) sin^n t cos^2 t dt =∫_0 ^(π/2) sin^n t(1−sin^2 t)dt = ∫_0 ^(π/2) sin^n t dt −∫_0 ^(π/2) sin^(n+2) dt =w_n −w_(n+2) let find w_n = ∫_0 ^(π/2) sin^n t dt we have w_n =∫_0 ^(π/2) sin^(n−2) t(1−cos^2 t)dt =w_(n−2) −∫_0 ^(π/2) cost( cost sin^(n−2) t)dt by parts u=cost and v^′ =cost sin^(n−2) t⇒ ∫_0 ^(π/2) cost (cost sin^(n−2) t)dt =[(1/(n−1)) cost sin^(n−1) t]_0 ^(π/2) −∫_0 ^(π/2) ((−sint)/(n−1)) sin^(n−1) tdt = ∫_0 ^(π/2) ((sin^n t)/(n−1)) dt =(1/(n−1)) w_n ⇒w_n =w_(n−2) −(1/(n−1)) w_n ⇒(1+(1/(n−1)))w_n =w_(n−2) ⇒ (n/(n−1))w_n =w_(n−2) ⇒w_n =((n−1)/n)w_(n−2) ⇒w_(2n) =((2n−1)/(2n))w_(2n−2) and w_(2n+1) =((2n)/(2n+1)) w_(2n−1) let find w_(2n) Π_(k=1) ^n w_(2k) =Π_(k=1) ^n ((2k−1)/(2k)) w_(2k−2) ⇒w_2 .w_4 .....w_(2n) =((1.3.5.....(2n−1))/((2)(4)....(2n)))w_0 w_2 ...w_(2n−2) ⇒ w_(2n) = ((1.3.5...(2n−1))/(2^n (n!))) w_0 = (((2n)!)/(2^(2n) (n!)^2 )) (π/2) let find w_(2n+1) I_(2n) =w_(2n) −w_(2n+2) = (((2n)!)/(2^(2n) (n!)^2 )) (π/2) − (((2n+4)!)/(2^(2n+4) {(n+2)!}^2 )) (π/2) let find w_(2n+1) we have w_(2n+1) =((2n)/(2n+1)) w_(2n−1) ⇒Π_(k=1) ^n w_(2k+1) =Π_(k=1) ^n ((2k)/(2k+1)) Π_(k=1) ^n w_(2k−1) ⇒ w_3 .w_5 .....w_(2n+1) =((2^n (n!))/(3.5....(2n+1))) w_1 .w_3 ....w_(2n−1) ⇒ w_(2n+1) = ((2^(2n) (n!)^2 )/((2n+1)!)) w_1 but w_1 =1 ⇒ I_(2n−1) =w_(2n−1) −w_(2n+1) =((2^(2n−2) {(n−1)!}^2 )/((2n−1)!)) −((2^(2n) (n!)^2 )/((2n+1)!)) .$
$c h a n g e m e n t x = s i n t g i v e I_{n} = \int_{0}^{\frac{π}{2}} {s i n}^{n} t {c o s}^{2} t d t$ $= \int_{0}^{\frac{π}{2}} {s i n}^{n} t (1 - {s i n}^{2} t) d t = \int_{0}^{\frac{π}{2}} {s i n}^{n} t d t - \int_{0}^{\frac{π}{2}} {s i n}^{n + 2} d t = w_{n} - w_{n + 2}$ $l e t f i n d w_{n} = \int_{0}^{\frac{π}{2}} {s i n}^{n} t d t w e h a v e w_{n} = \int_{0}^{\frac{π}{2}} {s i n}^{n - 2} t (1 - {c o s}^{2} t) d t$ $= w_{n - 2} - \int_{0}^{\frac{π}{2}} c o s t (c o s t {s i n}^{n - 2} t) d t b y p a r t s u = c o s t a n d v^{^{'}} = c o s t {s i n}^{n - 2} t \Rightarrow$ $\int_{0}^{\frac{π}{2}} c o s t (c o s t {s i n}^{n - 2} t) d t = {[\frac{1}{n - 1} c o s t {s i n}^{n - 1} t]}_{0}^{\frac{π}{2}} - \int_{0}^{\frac{π}{2}} \frac{- s i n t}{n - 1} {s i n}^{n - 1} t d t$ $= \int_{0}^{\frac{π}{2}} \frac{{s i n}^{n} t}{n - 1} d t = \frac{1}{n - 1} w_{n} \Rightarrow w_{n} = w_{n - 2} - \frac{1}{n - 1} w_{n} \Rightarrow (1 + \frac{1}{n - 1}) w_{n} = w_{n - 2} \Rightarrow$ $\frac{n}{n - 1} w_{n} = w_{n - 2} \Rightarrow w_{n} = \frac{n - 1}{n} w_{n - 2} \Rightarrow w_{2 n} = \frac{2 n - 1}{2 n} w_{2 n - 2} a n d$ $w_{2 n + 1} = \frac{2 n}{2 n + 1} w_{2 n - 1} l e t f i n d w_{2 n}$ $\prod_{k = 1}^{n} w_{2 k} = \prod_{k = 1}^{n} \frac{2 k - 1}{2 k} w_{2 k - 2} \Rightarrow w_{2} . w_{4} . . . . . w_{2 n} = \frac{1.3.5 . . . . . (2 n - 1)}{(2) (4) . . . . (2 n)} w_{0} w_{2} . . . w_{2 n - 2} \Rightarrow$ $w_{2 n} = \frac{1.3.5 . . . (2 n - 1)}{2^{n} (n!)} w_{0} = \frac{(2 n)!}{2^{2 n} {(n!)}^{2}} \frac{π}{2} l e t f i n d w_{2 n + 1}$ $I_{2 n} = w_{2 n} - w_{2 n + 2} = \frac{(2 n)!}{2^{2 n} {(n!)}^{2}} \frac{π}{2} - \frac{(2 n + 4)!}{2^{2 n + 4} {(n + 2)!}^{2}} \frac{π}{2} l e t f i n d w_{2 n + 1}$ $w e h a v e w_{2 n + 1} = \frac{2 n}{2 n + 1} w_{2 n - 1} \Rightarrow \prod_{k = 1}^{n} w_{2 k + 1} = \prod_{k = 1}^{n} \frac{2 k}{2 k + 1} \prod_{k = 1}^{n} w_{2 k - 1} \Rightarrow$ $w_{3} . w_{5} . . . . . w_{2 n + 1} = \frac{2^{n} (n!)}{3.5 . . . . (2 n + 1)} w_{1} . w_{3} . . . . w_{2 n - 1} \Rightarrow$ $w_{2 n + 1} = \frac{2^{2 n} {(n!)}^{2}}{(2 n + 1)!} w_{1} b u t w_{1} = 1 \Rightarrow I_{2 n - 1} = w_{2 n - 1} - w_{2 n + 1}$ $= \frac{2^{2 n - 2} {(n - 1)!}^{2}}{(2 n - 1)!} - \frac{2^{2 n} {(n!)}^{2}}{(2 n + 1)!} .$
Commented by maxmathsup by imad last updated on 05/Sep/18

$a n o t h e r w a y c h a n g e m e n t \sqrt{1 - x^{2}} = t g i v e x^{2} = 1 - t^{2} \Rightarrow d x = - d t \Rightarrow$ $I_{n} = \int_{0}^{1} {(1 - t^{2})}^{\frac{n}{2}} d t \Rightarrow I_{2 n} = \int_{0}^{1} {(1 - t^{2})}^{n} d t = \int_{0}^{1} \sum_{k = 0}^{n} C_{n}^{k} {(- 1)}^{k} t^{2 k} d t$ $= \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} \frac{1}{2 k + 1} = \sum_{k = 0}^{n} \frac{{(- 1)}^{k}}{2 k + 1} C_{n}^{k}$ $I_{2 n + 1} = \int_{0}^{1} {(1 - t^{2})}^{n + \frac{1}{2}} d t = \int_{0}^{1} {(1 - t^{2})}^{n} \sqrt{1 - t^{2}} d t$ $= \int_{0}^{1} \sqrt{1 - t^{2}} (\sum_{k = 0}^{n} C_{n}^{k} {(- 1)}^{k} t^{2 k}) d t$ $= \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} \int_{0}^{1} t^{2 k} \sqrt{1 - t^{2}} d t t h e n w e c a l c u l a t e w_{k} = \int_{0}^{1} t^{2 k} \sqrt{1 - t^{2}} d t$ $b y r e c u r r e n c e . . . .$
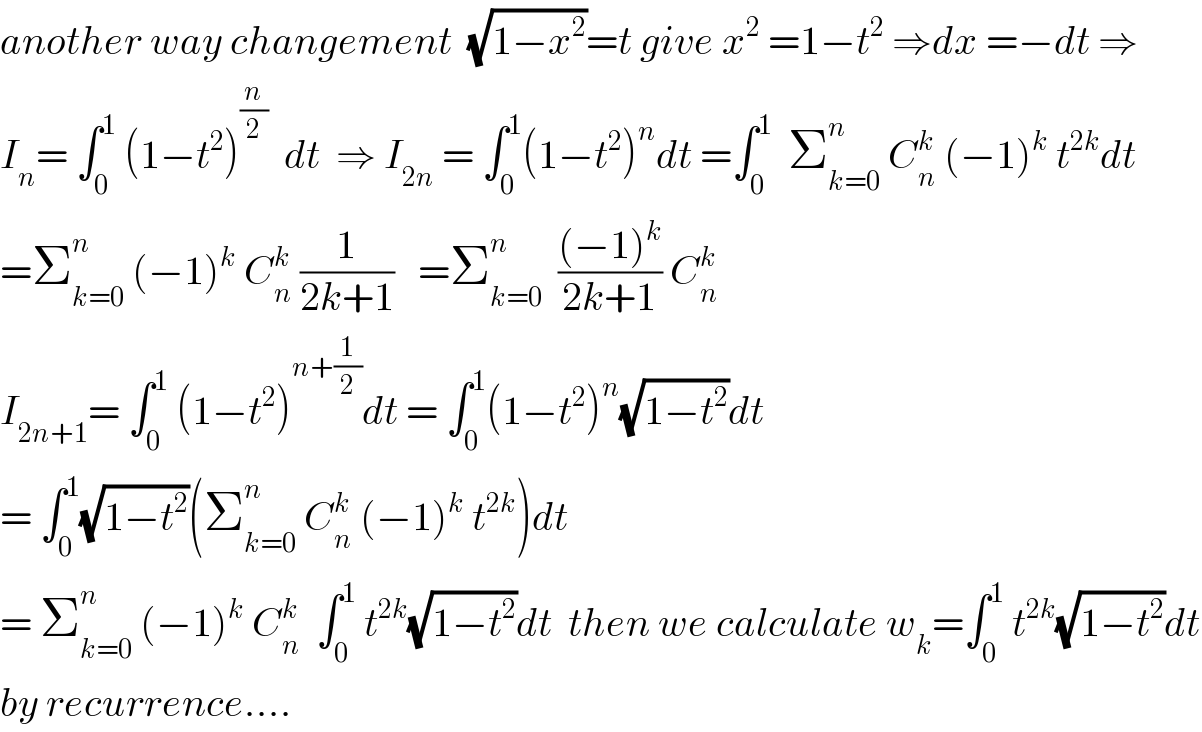
	Answered by tanmay.chaudhury50@gmail.com last updated on 03/Sep/18

	$x = s i n α d x = c o s α d α$ $\int_{0}^{\frac{Π}{2}} {s i n}^{n} α {c o s}^{2} α d α$ $u s i n g g a m m a b e t a f u n c t i o n$ $\int_{0}^{\frac{Π}{2}} {s i n}^{2 p - 1} α {c o s}^{2 q - 1} \propto d α$ $= \frac{⌈ p ⌈ q}{2 ⌈ (p + q)}$ $2 p - 1 = n p = \frac{n + 1}{2} 2 q - 1 = 2 q = \frac{3}{2}$ $\int_{0}^{\frac{Π}{2}} {s i n}^{2 \times \frac{n + 1}{2} - 1} α \times {c o s}^{2 \times \frac{3}{2} - 1} α d α$ $= \frac{⌈ (\frac{n + 1}{2}) \times ⌈ (\frac{3}{2})}{2 ⌈ (\frac{n + 4}{2})}$ $p l s c h e c k$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum