
Question and Answers Forum
Question Number 27999 by abdo imad last updated on 18/Jan/18
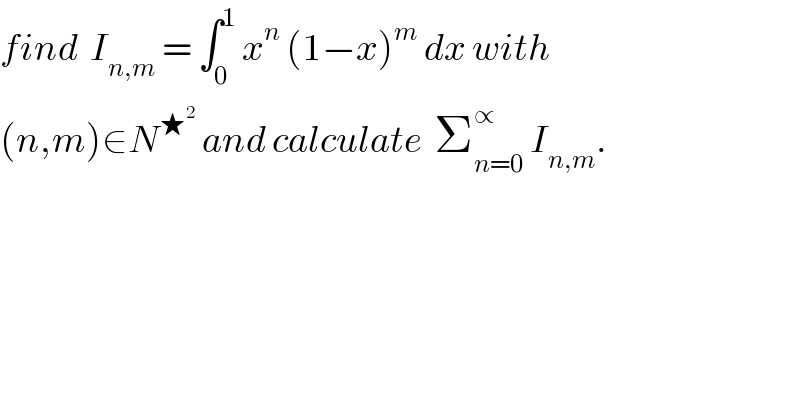
Commented by abdo imad last updated on 22/Jan/18
![due to uniform convergence we have Σ_(n=0) ^(+∞) I_(n,m) = ∫_0 ^1 (1−x)^m (Σ_(n=0) ^∝ x^n ) = ∫_0 ^1 (((1−x)^m )/(1−x))dx = ∫_0 ^1 (1−x)^(m−1) dx = [((−1)/m)(1−x)^m ]_0 ^1 = (1/m) for m≥1 .let calculate I_(n,m) by parts we have I_(n,m) = [−(1/(m+1)) x^n (1−x)^(m+1) ]_0 ^1 +(1/(m+1))∫_0 ^1 nx^(n−1) (1−x)^(m+1) dx =(n/(m+1)) ∫_0 ^1 x^(n−1) (1−x)^(m+1) dx I_(n,m) =(n/(m+1)) I_(n−1,m+1) = (n/(m+1)) ((n−1)/(m+2)) I_(n−2,m+2) =((n(n−1)....(n−p+1))/((m+1)(m+2)...(m+p))) I_(n−p,m+p) = ((n!)/((m+1)(m+2) ....(m+n))) I_(0,m+n) but I_(0,m+n) =∫_0 ^1 (1−x)^(m+n) dx =[((−1)/(m+n+1))(1−x)^(m+n+1) ]_0 ^1 = (1/(m+n+1)) so I_(n,m) = ((n!)/((m+1)(m+2)...(m+n+1))) I_(n,m) = (((n!)(m!))/((m+n+1)!)) .](Q28205.png)
| ||
Question and Answers Forum | ||
Question Number 27999 by abdo imad last updated on 18/Jan/18 | ||
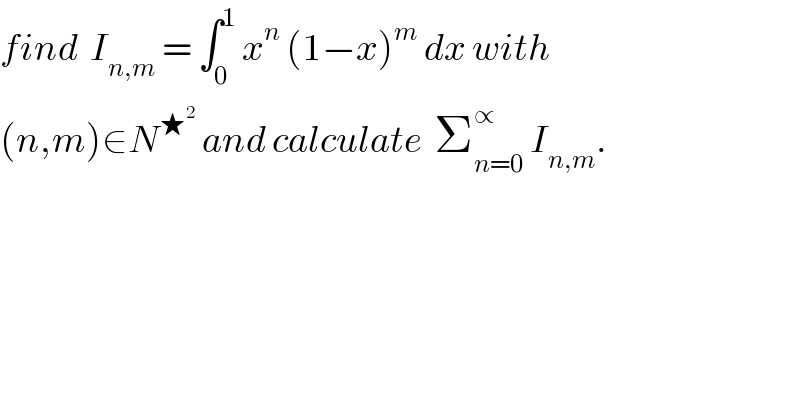 | ||
Commented by abdo imad last updated on 22/Jan/18 | ||
![due to uniform convergence we have Σ_(n=0) ^(+∞) I_(n,m) = ∫_0 ^1 (1−x)^m (Σ_(n=0) ^∝ x^n ) = ∫_0 ^1 (((1−x)^m )/(1−x))dx = ∫_0 ^1 (1−x)^(m−1) dx = [((−1)/m)(1−x)^m ]_0 ^1 = (1/m) for m≥1 .let calculate I_(n,m) by parts we have I_(n,m) = [−(1/(m+1)) x^n (1−x)^(m+1) ]_0 ^1 +(1/(m+1))∫_0 ^1 nx^(n−1) (1−x)^(m+1) dx =(n/(m+1)) ∫_0 ^1 x^(n−1) (1−x)^(m+1) dx I_(n,m) =(n/(m+1)) I_(n−1,m+1) = (n/(m+1)) ((n−1)/(m+2)) I_(n−2,m+2) =((n(n−1)....(n−p+1))/((m+1)(m+2)...(m+p))) I_(n−p,m+p) = ((n!)/((m+1)(m+2) ....(m+n))) I_(0,m+n) but I_(0,m+n) =∫_0 ^1 (1−x)^(m+n) dx =[((−1)/(m+n+1))(1−x)^(m+n+1) ]_0 ^1 = (1/(m+n+1)) so I_(n,m) = ((n!)/((m+1)(m+2)...(m+n+1))) I_(n,m) = (((n!)(m!))/((m+n+1)!)) .](Q28205.png) | ||