find f(a) =∫_1 ^2 arctan(x+(a/x))dx and calculate f^′ (a) at form of integral


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 68040 by mathmax by abdo last updated on 03/Sep/19

$f i n d f (a) = \int_{1}^{2} a r c t a n (x + \frac{a}{x}) d x a n d$ $c a l c u l a t e f^{^{'}} (a) a t f o r m o f i n t e g r a l$
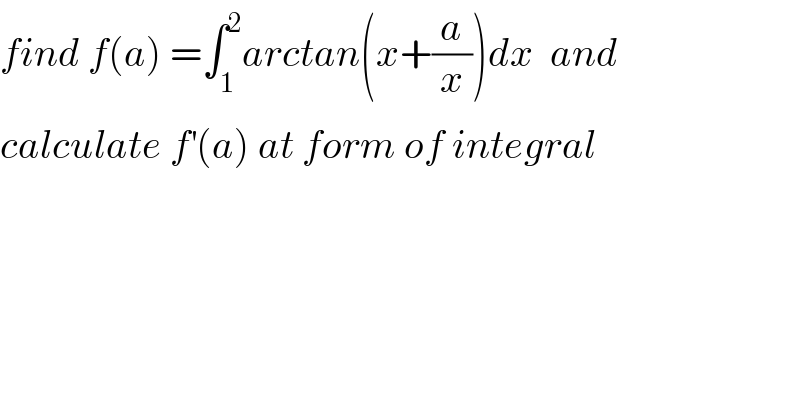
Commented by mathmax by abdo last updated on 04/Sep/19
$f(a) =∫_1 ^2 arctan(x+(a/x))dx by parts f(a) =[x arctan(x+(a/x))]_1 ^2 −∫_1 ^2 x((1−(a/x^2 ))/(1+(x+(a/x))^2 ))dx =2 arctan(2+(a/2))−arctan(1+a)−∫_1 ^2 ((x(x^2 −a))/(x^2 +(x^2 +a)^2 ))dx let J =∫_1 ^2 ((x^3 −ax)/(x^2 +(x^2 +a)^2 ))dx ⇒ J =∫_1 ^2 ((x^3 −ax)/(x^2 +x^4 +2ax^2 +a^2 ))dx =∫_1 ^2 ((x^3 −ax)/(x^4 +(2a+1)x^2 +a^2 )) x^4 +(2a+1)x^2 +a^2 =0 ⇒t^2 +(2a+1)t +a^2 =0 with t=x^2 Δ =(2a+1)^2 −4a^2 =4a^2 +4a +1−4a^2 =4a+1 case 1 if 4a+1≥0 ⇒ t_1 =((−(2a+1)+(√(4a+1)))/2) and t_2 =((−(2a+1)−(√(4a+1)))/2) ⇒x^4 +(2a+1)x^2 +a^2 =(t−t_1 )(t−t_2 ) (x^2 −t_1 )(x^2 −t_2 ) ⇒ J =(1/(t_1 −t_2 ))∫_1 ^2 (x^3 −ax){(1/(x^2 −t_1 ))−(1/(x^2 −t_2 ))}dx =(1/(√(4a+1))){ ∫_1 ^2 ((x^3 −ax)/(x^2 −t_1 ))dx −∫_1 ^2 ((x^3 −ax)/(x^2 −t_2 ))dx} we have ∫_1 ^2 ((x^3 −ax)/(x^2 −t_1 ))dx =∫_1 ^2 ((x(x^2 −t_1 )+xt_1 −ax)/(x^2 −t_1 ))dx =[(x^2 /2)]_1 ^2 +(t_1 −a) ∫_1 ^2 ((xdx)/(x^2 −t_1 )) =2−(1/2) +((t_1 −a)/2)[ln∣x^2 −t_1 ∣]_1 ^2 =(3/2) +((t_1 −a)/2){ln∣((4−t_1 )/(1−t_1 ))∣} also we get ∫_1 ^2 ((x^3 −ax)/(x^2 −t_2 )) dx =(3/2) +((t_2 −a)/2)ln∣((4−t_2 )/(1−t_2 ))∣ ⇒ J =(1/(√(4a+1))){(((t_1 −a))/2)ln∣((4−t_1 )/(1−t_1 ))∣−((t_2 −a)/2)ln∣((4−t_2 )/(1−t_2 ))∣} ⇒ f(a) =2arctan(2+(a/2))−arctan(1+a) −(1/(√(4a+1))){ ((t_1 −a)/2)ln∣((4−t_1 )/(1−t_1 ))∣−((t_2 −a)/2)ln∣((4−t_2 )/(1−t_2 ))∣}. rest to calculate f(a) if 4a+1<0 ??....becontinued...$
$f (a) = \int_{1}^{2} a r c t a n (x + \frac{a}{x}) d x b y p a r t s$ $f (a) = {[x a r c t a n (x + \frac{a}{x})]}_{1}^{2} - \int_{1}^{2} x \frac{1 - \frac{a}{x^{2}}}{1 + {(x + \frac{a}{x})}^{2}} d x$ $= 2 a r c t a n (2 + \frac{a}{2}) - a r c t a n (1 + a) - \int_{1}^{2} \frac{x (x^{2} - a)}{x^{2} + {(x^{2} + a)}^{2}} d x$ $l e t J = \int_{1}^{2} \frac{x^{3} - a x}{x^{2} + {(x^{2} + a)}^{2}} d x \Rightarrow J = \int_{1}^{2} \frac{x^{3} - a x}{x^{2} + x^{4} + 2 {a x}^{2} + a^{2}} d x$ $= \int_{1}^{2} \frac{x^{3} - a x}{x^{4} + (2 a + 1) x^{2} + a^{2}}$ $x^{4} + (2 a + 1) x^{2} + a^{2} = 0 \Rightarrow t^{2} + (2 a + 1) t + a^{2} = 0 w i t h t = x^{2}$ $Δ = {(2 a + 1)}^{2} - 4 a^{2} = 4 a^{2} + 4 a + 1 - 4 a^{2} = 4 a + 1$ $c a s e 1 i f 4 a + 1 ⩾ 0 \Rightarrow t_{1} = \frac{- (2 a + 1) + \sqrt{4 a + 1}}{2}$ $a n d t_{2} = \frac{- (2 a + 1) - \sqrt{4 a + 1}}{2} \Rightarrow x^{4} + (2 a + 1) x^{2} + a^{2}$ $= (t - t_{1}) (t - t_{2}) (x^{2} - t_{1}) (x^{2} - t_{2}) \Rightarrow$ $J = \frac{1}{t_{1} - t_{2}} \int_{1}^{2} (x^{3} - a x) {\frac{1}{x^{2} - t_{1}} - \frac{1}{x^{2} - t_{2}}} d x$ $= \frac{1}{\sqrt{4 a + 1}} {\int_{1}^{2} \frac{x^{3} - a x}{x^{2} - t_{1}} d x - \int_{1}^{2} \frac{x^{3} - a x}{x^{2} - t_{2}} d x} w e h a v e$ $\int_{1}^{2} \frac{x^{3} - a x}{x^{2} - t_{1}} d x = \int_{1}^{2} \frac{x (x^{2} - t_{1}) + {x t}_{1} - a x}{x^{2} - t_{1}} d x$ $= {[\frac{x^{2}}{2}]}_{1}^{2} + (t_{1} - a) \int_{1}^{2} \frac{x d x}{x^{2} - t_{1}} = 2 - \frac{1}{2} + \frac{t_{1} - a}{2} {[l n ∣ x^{2} - t_{1} ∣]}_{1}^{2}$ $= \frac{3}{2} + \frac{t_{1} - a}{2} {l n ∣ \frac{4 - t_{1}}{1 - t_{1}} ∣} a l s o w e g e t$ $\int_{1}^{2} \frac{x^{3} - a x}{x^{2} - t_{2}} d x = \frac{3}{2} + \frac{t_{2} - a}{2} l n ∣ \frac{4 - t_{2}}{1 - t_{2}} ∣ \Rightarrow$ $J = \frac{1}{\sqrt{4 a + 1}} {\frac{(t_{1} - a)}{2} l n ∣ \frac{4 - t_{1}}{1 - t_{1}} ∣ - \frac{t_{2} - a}{2} l n ∣ \frac{4 - t_{2}}{1 - t_{2}} ∣} \Rightarrow$ $f (a) = 2 a r c t a n (2 + \frac{a}{2}) - a r c t a n (1 + a)$ $- \frac{1}{\sqrt{4 a + 1}} {\frac{t_{1} - a}{2} l n ∣ \frac{4 - t_{1}}{1 - t_{1}} ∣ - \frac{t_{2} - a}{2} l n ∣ \frac{4 - t_{2}}{1 - t_{2}} ∣} .$ $r e s t t o c a l c u l a t e f (a) i f 4 a + 1 < 0 ? ? . . . . b e c o n t i n u e d . . .$
Commented by mathmax by abdo last updated on 05/Sep/19
$f^′ (a) =∫_1 ^2 (dx/(x(1+(x+(a/x))^2 ))) =∫_1 ^2 ((x^2 dx)/(x{x^2 +(x^2 +a)^2 })) =∫_1 ^2 ((xdx)/(x^2 +x^4 +2ax^2 +a^2 )) =∫_1 ^2 ((xdx)/(x^4 +(2a+1)x^2 +a^2 ))$
$f^{^{'}} (a) = \int_{1}^{2} \frac{d x}{x (1 + {(x + \frac{a}{x})}^{2})} = \int_{1}^{2} \frac{x^{2} d x}{x {x^{2} + {(x^{2} + a)}^{2}}}$ $= \int_{1}^{2} \frac{x d x}{x^{2} + x^{4} + 2 {a x}^{2} + a^{2}} = \int_{1}^{2} \frac{x d x}{x^{4} + (2 a + 1) x^{2} + a^{2}}$
	Answered by mind is power last updated on 03/Sep/19

	$i n t e g r a t i o n b y p a r t$ $f (s p a) = [x a r c t g (x + \frac{a}{x})] - \int x \frac{(1 - \frac{a}{x^{2}})}{1 + {(x + \frac{a}{x})}^{2}} d x$ $= 2 a r c t g (2 + \frac{a}{2}) - a r c t g (1 + a) - \int_{1}^{2} \frac{x (x^{2} - a)}{x^{4} + (2 a + 1) x^{2} + a^{2}} d x$ $u = x^{2}$ $d u = 2 x d x$ $f (a) = 2 a r c t v (2 + \frac{a}{2}) - a r c t g (1 + a) - \int_{1}^{4} \frac{(u - a) d u}{2 (u^{2} + (2 a + 1) u + a^{2})}$ $= 2 a r c t g (2 + \frac{a}{2}) - a r c t g (1 + a) - \int_{1}^{4} \frac{u + (a + \frac{1}{2}) - 2 a - \frac{1}{2}}{2 (u^{2} + (2 a + 1) u + a^{2}} d u$ $= 2 a r c t g (2 + \frac{a}{2}) - a r c t g (1 + a) - \int_{1}^{4} \frac{u + (a + \frac{1}{2})}{2 (u^{2} + (2 a + 1) u + a^{2}} d u + \frac{4 a + 1}{2} \int_{1}^{4} \frac{1}{{(u + \frac{2 a + 1}{2})}^{2} + a + \frac{1}{4}} d u$ $a > - \frac{1}{4}$ $= 2 a r c t g (2 + \frac{a}{2}) - a r c t g (1 + a) - \frac{1}{4} {[l n (u^{2} + (2 a + 1) u + a^{2})]}_{1}^{4} + 2 \int_{1}^{4} \frac{d u}{{(\frac{2 u}{\sqrt{4 a + 1}} + \frac{2 a + 1}{\sqrt{4 a + 1}})}^{2} + 1}$ $= 2 a r c t g (2 + \frac{a}{2}) - a r c t g (1 + a) - \frac{1}{4} l n (\frac{a^{2} + 8 a + 20}{a^{2} + 2 a + 2}) + \sqrt{4 a + 1} {[a r c t g (\frac{2 u}{\sqrt{4 a + 1}} + \frac{2 a + 1}{\sqrt{4 a + 1}})]}_{1}^{2}$ $b e e c o n t i n u e d$
	Commented by mathmax by abdo last updated on 04/Sep/19

	$t h a n k s s i r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum