
Question and Answers Forum
Question Number 67020 by mathmax by abdo last updated on 21/Aug/19
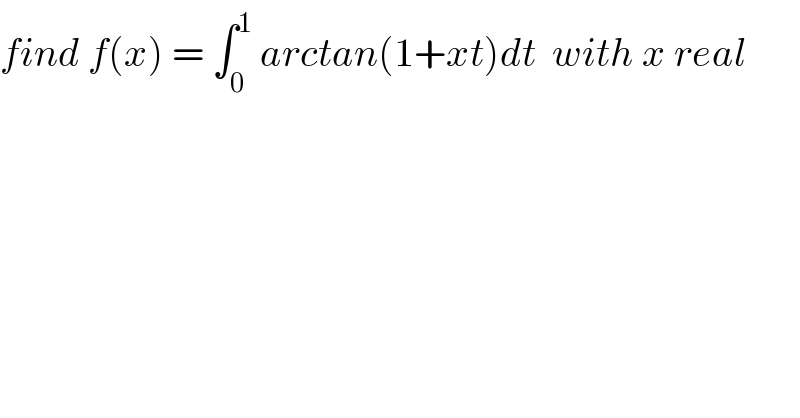
Commented by mathmax by abdo last updated on 22/Aug/19
![f(x)=∫_0 ^1 arctan(1+xt)dt by parts f(x) =t arctan(1+xt)]_0 ^1 −∫_0 ^1 t (x/(1+(1+xt)^2 ))dt =arctan(1+x)−x ∫_0 ^1 (t/(1+(1+xt)^2 ))dt but ∫_0 ^1 (t/(1+(1+xt)^2 ))dt =∫_0 ^1 ((tdt)/(1+1+2xt +x^2 t^2 )) =∫_0 ^1 ((tdt)/(x^2 t^2 +2xt +2)) let decompose F(t)=(t/(x^2 t^2 +2xt+2)) Δ^′ =x^2 −2x^2 =−x^2 <0 if x≠0 so F(t) =(t/(x^2 (t^2 +((2t)/x)+(2/x^2 )))) =(t/(x^2 (t^2 +((2t)/x) +(1/x^2 ) +(2/x^2 )−(1/x^2 )))) =(t/(x^2 {(t+(1/x))^2 +(1/x^2 )})) we use the changement t+(1/x) =(1/(∣x∣))u ⇒xt+1=s(x)u ∫_(s(x)) ^((x+1)s(x)) (t/(1+(1+tx)^2 ))dt =∫_(s(x)) ^((x+1)s(x)) ((((1/(∣x∣))u−(1/x)))/(x^2 ×(1/x^2 )(1+u^2 )))du =(1/(∣x∣))∫_(s(x)) ^((x+1)s(x)) (u/(1+u^2 ))−(1/x) ∫_(s(x)) ^((x+1)s(x)) (du/(1+u^2 )) =(1/(2∣x∣))[ln(1+u^2 )]_(s(x)) ^((x+1)s(x)) −(1/x)[arctanu]_(s(x)) ^((x+1)s(x)) (s^2 (x)=1) =(1/(2∣x∣)){ln(1+(x+1)^2 )−ln2}−(1/x){arctan(x+1)s(x)−arctan(s(x))} ⇒f(x)= arctan(1+x)−((s(x))/2){ln(x^2 +2x+2)−ln(2)} +arctan(x+1)s(x)+x arctan(s(x)) with s(x) =1 if x>0 and s(x)=−1 if x<0](Q67080.png)
| ||
Question and Answers Forum | ||
Question Number 67020 by mathmax by abdo last updated on 21/Aug/19 | ||
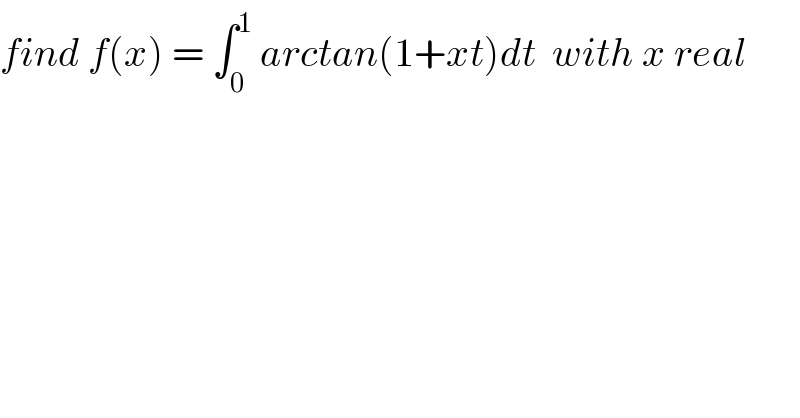 | ||
Commented by mathmax by abdo last updated on 22/Aug/19 | ||
![f(x)=∫_0 ^1 arctan(1+xt)dt by parts f(x) =t arctan(1+xt)]_0 ^1 −∫_0 ^1 t (x/(1+(1+xt)^2 ))dt =arctan(1+x)−x ∫_0 ^1 (t/(1+(1+xt)^2 ))dt but ∫_0 ^1 (t/(1+(1+xt)^2 ))dt =∫_0 ^1 ((tdt)/(1+1+2xt +x^2 t^2 )) =∫_0 ^1 ((tdt)/(x^2 t^2 +2xt +2)) let decompose F(t)=(t/(x^2 t^2 +2xt+2)) Δ^′ =x^2 −2x^2 =−x^2 <0 if x≠0 so F(t) =(t/(x^2 (t^2 +((2t)/x)+(2/x^2 )))) =(t/(x^2 (t^2 +((2t)/x) +(1/x^2 ) +(2/x^2 )−(1/x^2 )))) =(t/(x^2 {(t+(1/x))^2 +(1/x^2 )})) we use the changement t+(1/x) =(1/(∣x∣))u ⇒xt+1=s(x)u ∫_(s(x)) ^((x+1)s(x)) (t/(1+(1+tx)^2 ))dt =∫_(s(x)) ^((x+1)s(x)) ((((1/(∣x∣))u−(1/x)))/(x^2 ×(1/x^2 )(1+u^2 )))du =(1/(∣x∣))∫_(s(x)) ^((x+1)s(x)) (u/(1+u^2 ))−(1/x) ∫_(s(x)) ^((x+1)s(x)) (du/(1+u^2 )) =(1/(2∣x∣))[ln(1+u^2 )]_(s(x)) ^((x+1)s(x)) −(1/x)[arctanu]_(s(x)) ^((x+1)s(x)) (s^2 (x)=1) =(1/(2∣x∣)){ln(1+(x+1)^2 )−ln2}−(1/x){arctan(x+1)s(x)−arctan(s(x))} ⇒f(x)= arctan(1+x)−((s(x))/2){ln(x^2 +2x+2)−ln(2)} +arctan(x+1)s(x)+x arctan(s(x)) with s(x) =1 if x>0 and s(x)=−1 if x<0](Q67080.png) | ||