Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 38453 by maxmathsup by imad last updated on 25/Jun/18

$$findf\left(x\right)={\int }_0^{\mathrm{\infty }}\frac{1-cos\left(xt\right)}{t}{e}^{-xt}dtwithx>0$$$$1)findasimpleformoff\left(x\right)$$$$2)calculate{\int }_0^{\mathrm{\infty }}\frac{1-cos\left(\pi t\right)}{t}{e}^{-t}dt$$$$3)calculate{\int }_0^{\mathrm{\infty }}\frac{1-cos\left(3t\right)}{t}{e}^{-2t}dt$$

Commented by math khazana by abdo last updated on 26/Jun/18

$$theQisfindf\left(x\right)={\int }_0^{\mathrm{\infty }}\frac{1-cos\left(at\right)}{t}{e}^{-xt}dt$$

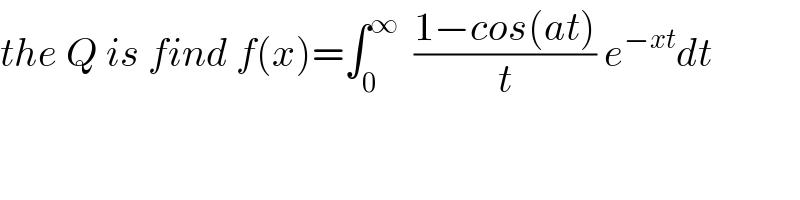
Commented by math khazana by abdo last updated on 29/Jun/18

$$1)wehavef\left(x\right)={\int }_0^{\mathrm{\infty }}\frac{1-cos\left(at\right)}{t}{e}^{-xt}dt\Rightarrow$$$$f^{{}^{\prime }}\left(x\right)=-{\int }_0^{\mathrm{\infty }}(1-cos\left(at\right))e^{-xt}dt$$$$={\int }_0^{\mathrm{\infty }}cos\left(at\right)e^{-xt}dt-{\int }_0^{\mathrm{\infty }}{e}^{-xt}dtbut$$$${\int }_0^{\mathrm{\infty }}{e}^{-xt}dt={[-\frac{1}{x}{e}^{-xt}]}_0^{+\mathrm{\infty }}=\frac{1}{x}$$$${\int }_0^{\mathrm{\infty }}cos\left(at\right)e^{-xt}dt=Re\left({\int }_0^{\mathrm{\infty }}{e}^{iat-xt}dt\right)$$$${\int }_0^{\mathrm{\infty }}{e}^{(-x+ia)t}dt={\left[\frac{1}{-x+ia}{e}^{(-x+ia)t}\right]}_0^{+\mathrm{\infty }}$$$$=\frac{-1}{-x+ia}=\frac{1}{x-ia}=\frac{x+ia}{x^2+a^2}\Rightarrow$$$${\int }_0^{\mathrm{\infty }}cos\left(at\right)e^{-xt}dt=\frac{x}{x^2+a^2}\Rightarrow$$$$f^{{}^{\prime }}\left(x\right)=\frac{x}{x^2+a^2}-\frac{1}{x}\Rightarrow$$$$f\left(x\right)=\frac{1}{2}ln(x^2+a^2)-ln\left(x\right)+cbut\mathrm{\exists }m>0<$$$$\mid {\int }_0^{\mathrm{\infty }}\frac{1-cos\left(at\right)}{t}{e}^{-xt}dt\mid ⩽m{\int }_0^{\mathrm{\infty }}{e}^{-xt}dt=\frac{m}{x}\to 0$$$$whenx\to +\mathrm{\infty }alsowehave$$$$f\left(x\right)=\frac{1}{2}ln\left(\frac{x^2+a^2}{x^2}\right)+c\Rightarrow$$$$c={lim}_{x\to +\mathrm{\infty }}f\left(x\right)-\frac{1}{2}ln\left(\frac{x^2+a^2}{x^2}\right)=0\Rightarrow$$$$f\left(x\right)=\frac{1}{2}ln(x^2+a^2)-ln\left(x\right)withx>0$$

Commented by math khazana by abdo last updated on 29/Jun/18

$$2)wehaveprovedthat$$$${\int }_0^{\mathrm{\infty }}\frac{1-cos\left(at\right)}{t}{e}^{-xt}dt=\frac{1}{2}ln(x^2+a^2)-ln\left(x\right)\Rightarrow$$$${\int }_0^{\mathrm{\infty }}\frac{1-cos\left(\pi t\right)}{t}{e}^{-t}=\frac{1}{2}ln(1+{\pi }^2).$$

Commented by math khazana by abdo last updated on 29/Jun/18

$$3)?{\int }_0^{\mathrm{\infty }}\frac{1-cos\left(3t\right)}{t}{e}^{-2t}dt=\frac{1}{2}ln(2^2+3^2)-ln\left(2\right)$$$$=\frac{1}{2}ln\left(13\right)-ln\left(2\right).$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com