
Question and Answers Forum
Question Number 85236 by jagoll last updated on 20/Mar/20
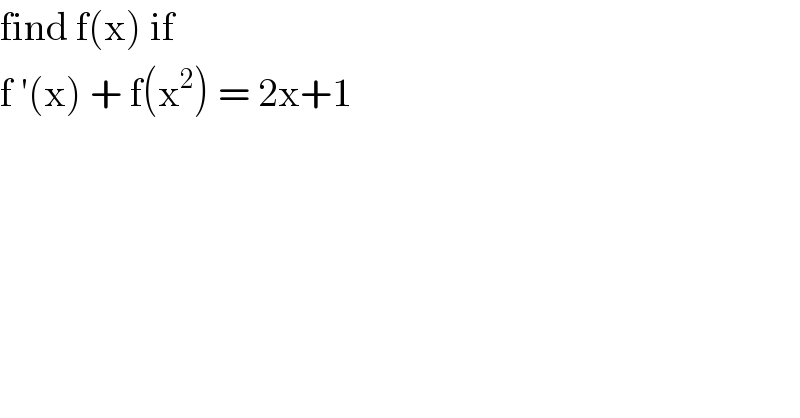
Commented by mathmax by abdo last updated on 20/Mar/20
![its clear that f is polynomial let f(x)=Σ_(n=0) ^∞ a_n x^n f^′ (x) =Σ_(n=1) ^∞ na_n x^(n−1) =Σ_(n=0) ^∞ (n+1)a_(n+1) x^n f(x^2 ) =Σ_(n=0) ^∞ a_n x^(2n) ⇒ Σ_(n=0) ^∞ (n+1)a_(n+1) x^n +Σ_(n=0) ^∞ a_n x^(2n) =2x+1 changement of indice 2n =p ⇒Σ_(n=0) ^∞ (n+1)a_n x^n +Σ_(p=0) ^∞ a_([(p/2)]) x^p =2x+1 ⇒ Σ_(n=0) ^∞ {(n+1)a_n +a_([(n/2)]) }x^n =2x+1 ⇒ { ((a_0 +a_0 =1)),((2a_1 +a_0 =2 and (n+1)a_n +a_([(n/2)]) =0 ∀n≥2 ⇒)) :} { ((a_0 =(1/2) and a_n =−(a_([(n/2)]) /(n+1)) ∀n≥2)),((a_1 =(3/4))) :} a_2 =−(a_1 /3) , a_3 =−(a_1 /4) .....](Q85310.png)
Answered by john santu last updated on 20/Mar/20
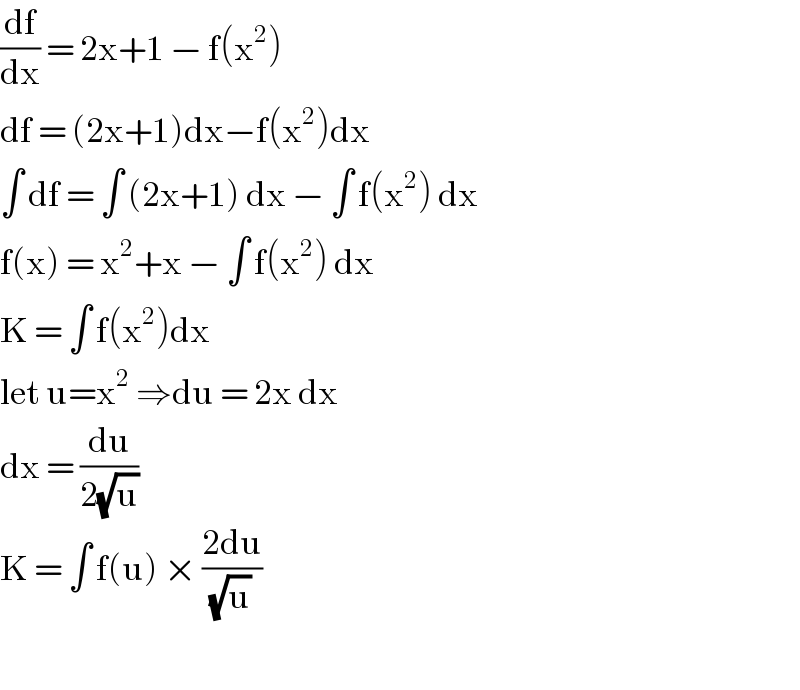
Commented by jagoll last updated on 20/Mar/20
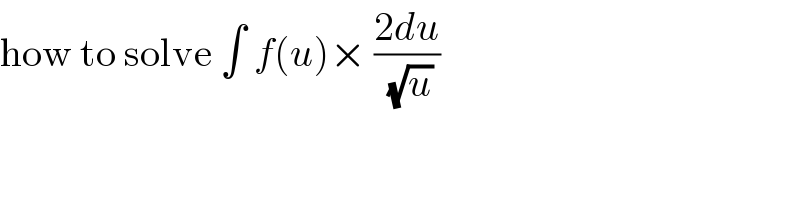
| ||
Question and Answers Forum | ||
Question Number 85236 by jagoll last updated on 20/Mar/20 | ||
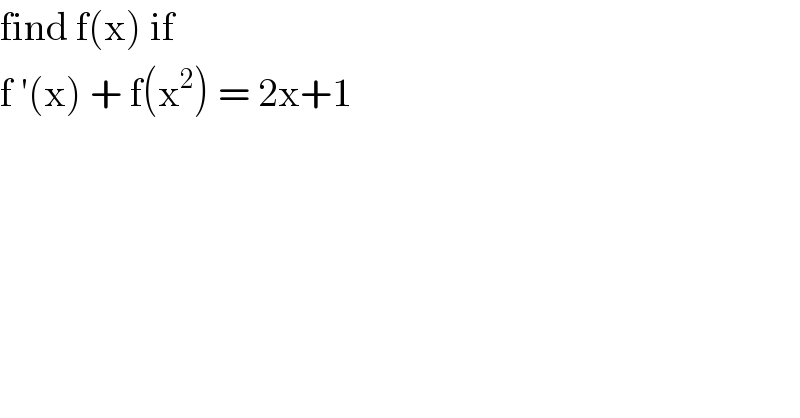 | ||
Commented by mathmax by abdo last updated on 20/Mar/20 | ||
![its clear that f is polynomial let f(x)=Σ_(n=0) ^∞ a_n x^n f^′ (x) =Σ_(n=1) ^∞ na_n x^(n−1) =Σ_(n=0) ^∞ (n+1)a_(n+1) x^n f(x^2 ) =Σ_(n=0) ^∞ a_n x^(2n) ⇒ Σ_(n=0) ^∞ (n+1)a_(n+1) x^n +Σ_(n=0) ^∞ a_n x^(2n) =2x+1 changement of indice 2n =p ⇒Σ_(n=0) ^∞ (n+1)a_n x^n +Σ_(p=0) ^∞ a_([(p/2)]) x^p =2x+1 ⇒ Σ_(n=0) ^∞ {(n+1)a_n +a_([(n/2)]) }x^n =2x+1 ⇒ { ((a_0 +a_0 =1)),((2a_1 +a_0 =2 and (n+1)a_n +a_([(n/2)]) =0 ∀n≥2 ⇒)) :} { ((a_0 =(1/2) and a_n =−(a_([(n/2)]) /(n+1)) ∀n≥2)),((a_1 =(3/4))) :} a_2 =−(a_1 /3) , a_3 =−(a_1 /4) .....](Q85310.png) | ||
Answered by john santu last updated on 20/Mar/20 | ||
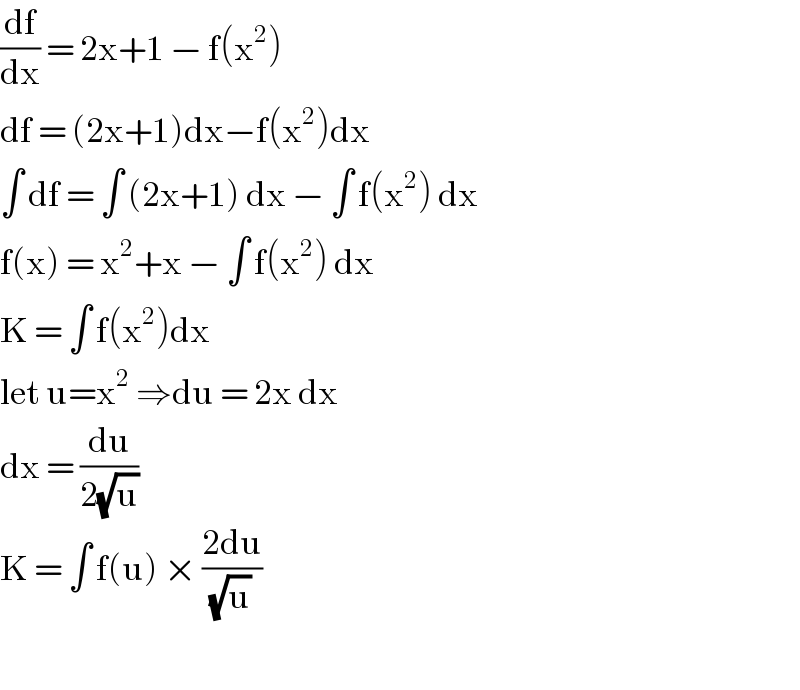 | ||
| ||
Commented by jagoll last updated on 20/Mar/20 | ||
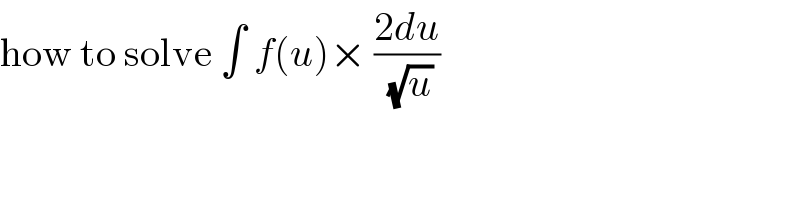 | ||