
Question and Answers Forum
Question Number 29162 by abdo imad last updated on 04/Feb/18
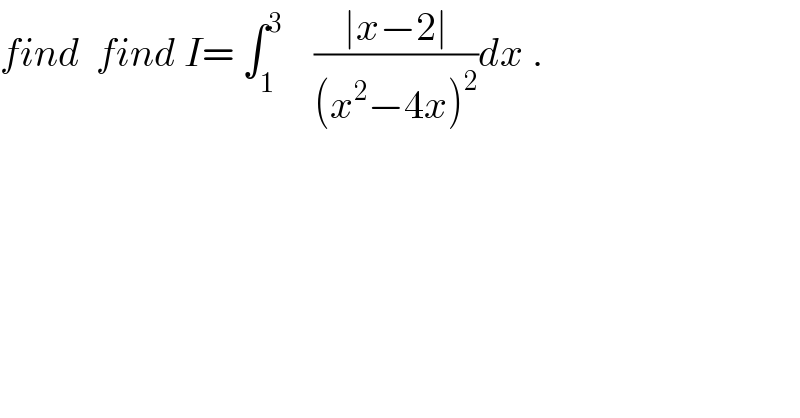
Commented by abdo imad last updated on 06/Feb/18
![the chasles relation give I=∫_1 ^2 ((−x+2)/((x^2 −4x)^2 ))dx +∫_2 ^3 ((x−2)/((x^2 −4x)^2 ))dx ∫_1 ^2 ((−x +2)/((x^2 −4x)^2 ))dx=−(1/2)∫_1 ^2 ((2x−4)/((x^2 −4x)^2 ))dx =(1/2)[ (1/(x^2 −4x))]_1 ^2 =(1/2)(−(1/4) +(1/3))=(1/(24)) and ∫_2 ^3 ((x−2)/((x^2 −4x)^2 ))dx=(1/2) ∫_1 ^3 ((2x−4)/((x^2 −4x)^2 ))dx =−(1/2)[ (1/(x^2 −4x))]_1 ^3 =−(1/2)( −(1/3) +(1/3))=0 ⇒ I=(1/(24)) .](Q29304.png)
| ||
Question and Answers Forum | ||
Question Number 29162 by abdo imad last updated on 04/Feb/18 | ||
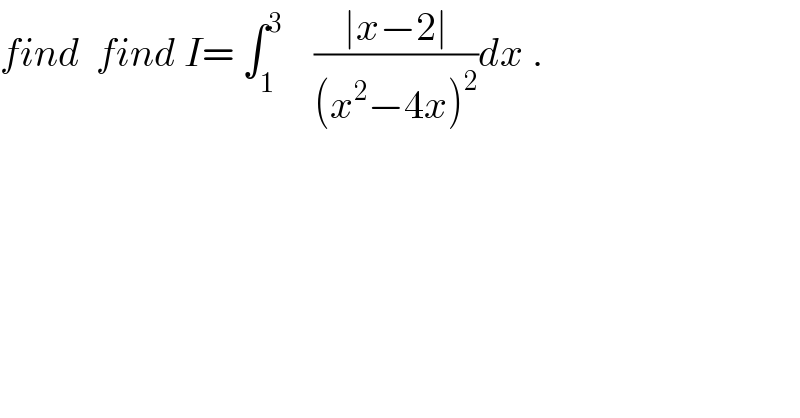 | ||
Commented by abdo imad last updated on 06/Feb/18 | ||
![the chasles relation give I=∫_1 ^2 ((−x+2)/((x^2 −4x)^2 ))dx +∫_2 ^3 ((x−2)/((x^2 −4x)^2 ))dx ∫_1 ^2 ((−x +2)/((x^2 −4x)^2 ))dx=−(1/2)∫_1 ^2 ((2x−4)/((x^2 −4x)^2 ))dx =(1/2)[ (1/(x^2 −4x))]_1 ^2 =(1/2)(−(1/4) +(1/3))=(1/(24)) and ∫_2 ^3 ((x−2)/((x^2 −4x)^2 ))dx=(1/2) ∫_1 ^3 ((2x−4)/((x^2 −4x)^2 ))dx =−(1/2)[ (1/(x^2 −4x))]_1 ^3 =−(1/2)( −(1/3) +(1/3))=0 ⇒ I=(1/(24)) .](Q29304.png) | ||