
Question and Answers Forum
Question Number 146758 by tabata last updated on 15/Jul/21
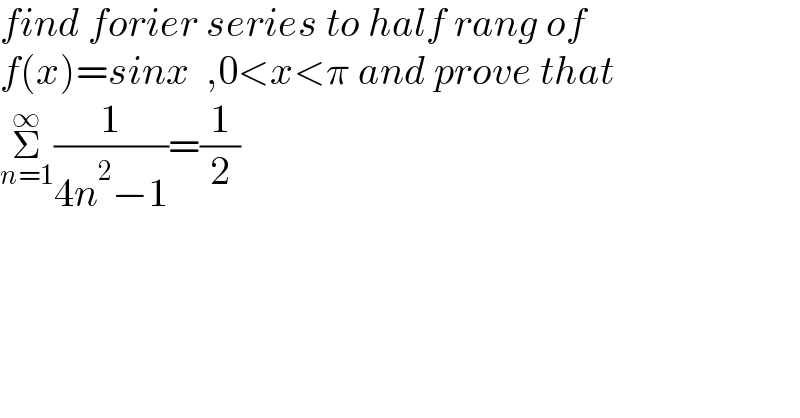
Answered by Olaf_Thorendsen last updated on 15/Jul/21
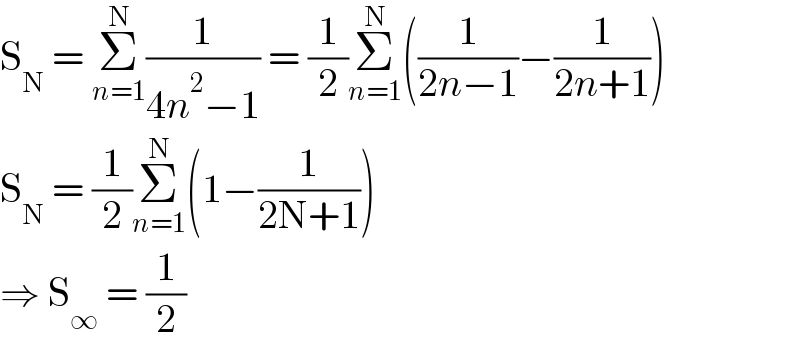
Commented by tabata last updated on 15/Jul/21

Answered by Olaf_Thorendsen last updated on 15/Jul/21
![f(x) = sinx, 0<x<π a_0 = (2/π)∫_0 ^π f(x) dx = (2/π)∫_0 ^π sinx dx a_0 = (2/π)[−cosx]_0 ^π = (4/π) a_1 = (2/π)∫_0 ^π sinxcos dx = (1/π)∫_0 ^π sin(2x)dx a_1 = 0 n > 1 : a_n = (2/π)∫_0 ^π f(x)cos(((nπx)/π)) dx a_n = (2/π)∫_0 ^π sinxcos(nx) dx a_n = (2/π)∫_0 ^π (1/2)[sin((n+1)x)−sin((n−1)x)] dx a_n = (2/π)∫_0 ^π (1/2)[sin((n+1)x)−sin((n−1)x)] dx a_n = (1/π)[−((cos((n+1)x))/(n+1))+((cos((n−1)x))/(n−1))]_0 ^π a_n = (1/π)[−(((−1)^(n+1) )/(n+1))+(((−1)^(n−1) )/(n−1))+(1/(n+1))−(1/(n−1))] a_n = −(2/(π(n^2 −1)))[(−1)^n +1] sinx = (a_0 /2)+a_1 cosx+Σ_(n=2) ^∞ a_n cos(nx) sinx = (2/π)−(2/π)Σ_(n=2) ^∞ (((−1)^n +1)/(n^2 −1))cos(nx) n = 2m sinx = (2/π)−(4/π)Σ_(m=1) ^∞ (1/(4m^2 −1))cos(2mx) x = 0 : 0 = (2/π)−(4/π)Σ_(m=1) ^∞ (1/(4m^2 −1)) Σ_(m=1) ^∞ (1/(4m^2 −1)) = (1/2)](Q146766.png)
| ||
Question and Answers Forum | ||
Question Number 146758 by tabata last updated on 15/Jul/21 | ||
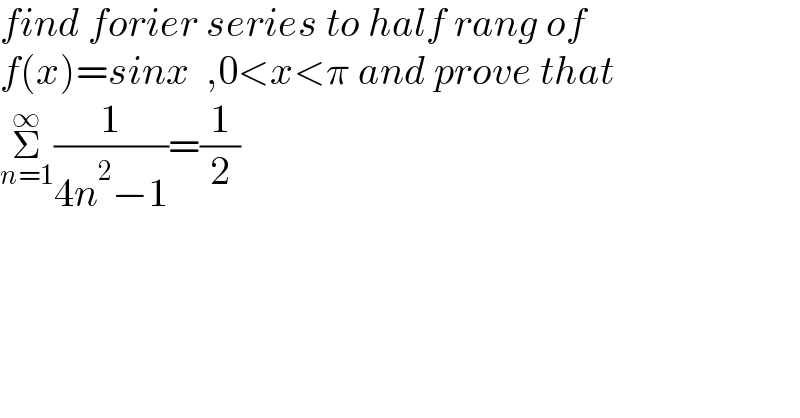 | ||
Answered by Olaf_Thorendsen last updated on 15/Jul/21 | ||
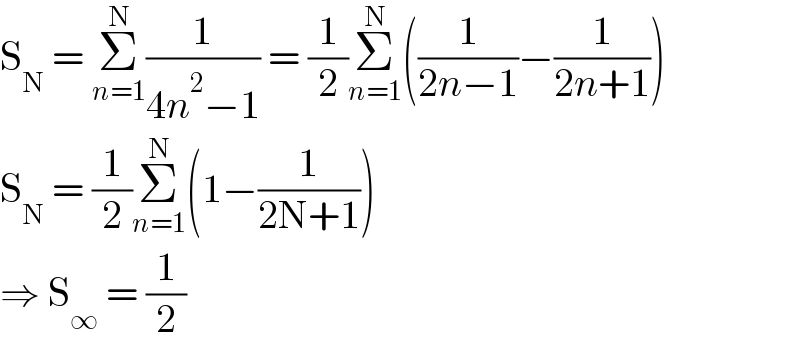 | ||
| ||
Commented by tabata last updated on 15/Jul/21 | ||
 | ||
Answered by Olaf_Thorendsen last updated on 15/Jul/21 | ||
![f(x) = sinx, 0<x<π a_0 = (2/π)∫_0 ^π f(x) dx = (2/π)∫_0 ^π sinx dx a_0 = (2/π)[−cosx]_0 ^π = (4/π) a_1 = (2/π)∫_0 ^π sinxcos dx = (1/π)∫_0 ^π sin(2x)dx a_1 = 0 n > 1 : a_n = (2/π)∫_0 ^π f(x)cos(((nπx)/π)) dx a_n = (2/π)∫_0 ^π sinxcos(nx) dx a_n = (2/π)∫_0 ^π (1/2)[sin((n+1)x)−sin((n−1)x)] dx a_n = (2/π)∫_0 ^π (1/2)[sin((n+1)x)−sin((n−1)x)] dx a_n = (1/π)[−((cos((n+1)x))/(n+1))+((cos((n−1)x))/(n−1))]_0 ^π a_n = (1/π)[−(((−1)^(n+1) )/(n+1))+(((−1)^(n−1) )/(n−1))+(1/(n+1))−(1/(n−1))] a_n = −(2/(π(n^2 −1)))[(−1)^n +1] sinx = (a_0 /2)+a_1 cosx+Σ_(n=2) ^∞ a_n cos(nx) sinx = (2/π)−(2/π)Σ_(n=2) ^∞ (((−1)^n +1)/(n^2 −1))cos(nx) n = 2m sinx = (2/π)−(4/π)Σ_(m=1) ^∞ (1/(4m^2 −1))cos(2mx) x = 0 : 0 = (2/π)−(4/π)Σ_(m=1) ^∞ (1/(4m^2 −1)) Σ_(m=1) ^∞ (1/(4m^2 −1)) = (1/2)](Q146766.png) | ||
| ||