
Question and Answers Forum
Question Number 67235 by prof Abdo imad last updated on 24/Aug/19
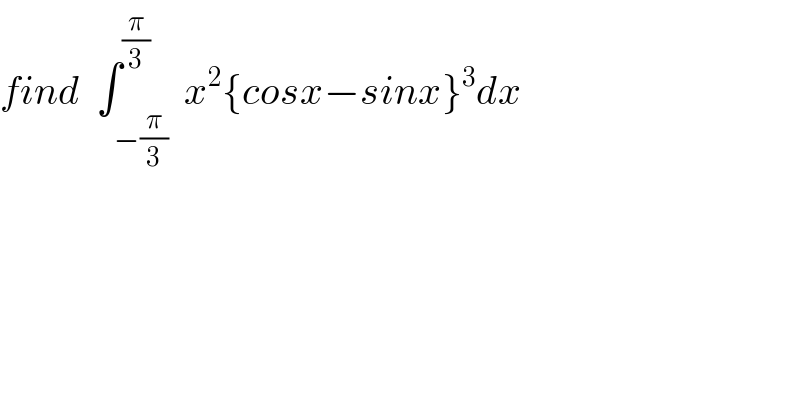
Commented by mathmax by abdo last updated on 01/Sep/19
![let I =∫_(−(π/3)) ^(π/3) x^2 {cosx −sinx}^3 and J=∫_(−(π/6)) ^(π/6) x^2 {cosx +sinx}^3 dx we have I +J =∫_(−(π/3)) ^(π/3) x^2 (cosx −sinx +cosx +sinx)((cosx−sinx)^2 −(cosx−sinx)(cosx +sinx)+(cosx +sinx)^2 }dx =∫_(−(π/3)) ^(π/3) 2x^2 cosx{1−2cosxsinx −(cos^2 x−sin^2 x) +1+2cosx sinx}dx =∫_(−(π/3)) ^(π/3) 2x^2 cosx{2 −cos(2x)}dx =4 ∫_0 ^(π/3) x^2 cosx(2−cos(2x))dx =8 ∫_0 ^(π/3) x^2 cosxdx −4∫_0 ^(π/3) cosx.cos(2x)dx by parts ∫_0 ^(π/3) x^2 cosxdx=[x^2 sinx]_0 ^(π/3) −∫_0 ^(π/3) 2xsinx dx =−2{[−xcosx]_0 ^(π/3) −∫_0 ^(π/3) (−cosx)dx} =−2{−(π/6) +[sinx]_0 ^(π/3) }=−2{−(π/6)+((√3)/2)} =(π/3)−(√3) ∫_0 ^(π/3) cosx cos(2x)dx =(1/2)∫_0 ^(π/3) (cos(3x)+cosx)dx=(1/6)[sin(3x)]_0 ^(π/3) +(1/2)[sinx]_0 ^(π/3) =(1/2)((√3)/2) =((√3)/4) ⇒ I+J =8((π/3)−(√3))−(√3) =((8π)/3)−9(√3) I−J =∫_(−(π/3)) ^(π/3) x^2 {(cosx−sinx)^3 −(cosx+sinx)^3 }dx =∫_(−(π/3)) ^(π/3) x^2 (−2sinx)(1−2cosx sinx +cos(2x) +1+2cosxsinx}dx =−2∫_(−(π/3)) ^(π/3) x^2 sinx{2+cos(2x)}dx =0 because the function is odd ⇒I−J =0 ⇒I =J ⇒ ⇒2I =((8π)/3)−9(√3) ⇒I =((4π)/3)−(9/2)(√3)](Q67892.png)
| ||
Question and Answers Forum | ||
Question Number 67235 by prof Abdo imad last updated on 24/Aug/19 | ||
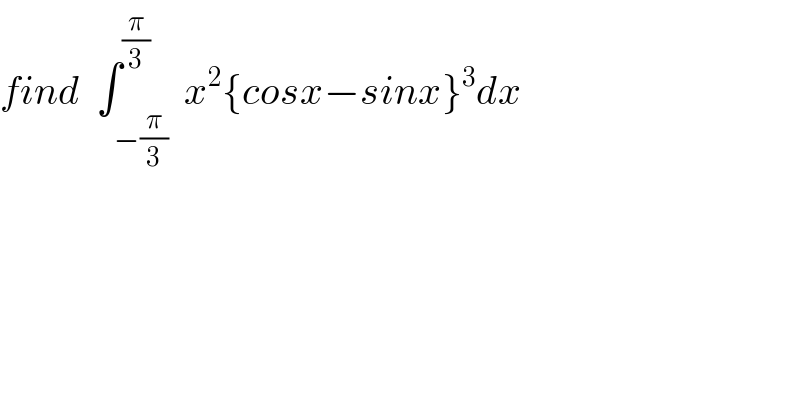 | ||
Commented by mathmax by abdo last updated on 01/Sep/19 | ||
![let I =∫_(−(π/3)) ^(π/3) x^2 {cosx −sinx}^3 and J=∫_(−(π/6)) ^(π/6) x^2 {cosx +sinx}^3 dx we have I +J =∫_(−(π/3)) ^(π/3) x^2 (cosx −sinx +cosx +sinx)((cosx−sinx)^2 −(cosx−sinx)(cosx +sinx)+(cosx +sinx)^2 }dx =∫_(−(π/3)) ^(π/3) 2x^2 cosx{1−2cosxsinx −(cos^2 x−sin^2 x) +1+2cosx sinx}dx =∫_(−(π/3)) ^(π/3) 2x^2 cosx{2 −cos(2x)}dx =4 ∫_0 ^(π/3) x^2 cosx(2−cos(2x))dx =8 ∫_0 ^(π/3) x^2 cosxdx −4∫_0 ^(π/3) cosx.cos(2x)dx by parts ∫_0 ^(π/3) x^2 cosxdx=[x^2 sinx]_0 ^(π/3) −∫_0 ^(π/3) 2xsinx dx =−2{[−xcosx]_0 ^(π/3) −∫_0 ^(π/3) (−cosx)dx} =−2{−(π/6) +[sinx]_0 ^(π/3) }=−2{−(π/6)+((√3)/2)} =(π/3)−(√3) ∫_0 ^(π/3) cosx cos(2x)dx =(1/2)∫_0 ^(π/3) (cos(3x)+cosx)dx=(1/6)[sin(3x)]_0 ^(π/3) +(1/2)[sinx]_0 ^(π/3) =(1/2)((√3)/2) =((√3)/4) ⇒ I+J =8((π/3)−(√3))−(√3) =((8π)/3)−9(√3) I−J =∫_(−(π/3)) ^(π/3) x^2 {(cosx−sinx)^3 −(cosx+sinx)^3 }dx =∫_(−(π/3)) ^(π/3) x^2 (−2sinx)(1−2cosx sinx +cos(2x) +1+2cosxsinx}dx =−2∫_(−(π/3)) ^(π/3) x^2 sinx{2+cos(2x)}dx =0 because the function is odd ⇒I−J =0 ⇒I =J ⇒ ⇒2I =((8π)/3)−9(√3) ⇒I =((4π)/3)−(9/2)(√3)](Q67892.png) | ||