
Question and Answers Forum
Question Number 33328 by prof Abdo imad last updated on 14/Apr/18
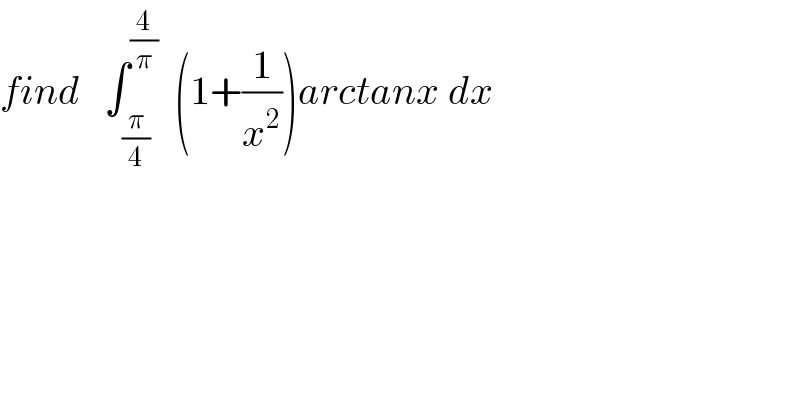
Commented by math khazana by abdo last updated on 19/Apr/18
![let put I = ∫_(π/4) ^(4/π) (1+(1/x^2 ))arctanx dx .let integrate by parts u^′ =1+(1/x^2 ) and v =arctanx I = [(1−(1/x))arctanx]_(π/4) ^(4/π) −∫_(π/4) ^(4/π) (1−(1/x)) (dx/(1+x^2 )) = (1−(π/4))arctan((4/π)) −(1−(4/π)) −∫_(π/4) ^(4/π) (dx/(1+x^2 )) + ∫_(π/4) ^(4/π) (dx/(x( 1+x^2 ))) but ∫_(π/4) ^(4/π) (dx/(1+x^2 )) = arctan( (4/π)) −arctan((π/4)) =(π/2) −1−1=(π/2) −2 let?decompose F(x) = (1/(x(1+x^2 ))) = (a/x) +((bx +c)/(1+x^2 )) a =lim_(x→0) x F(x) = 1 lim_(x→+∞) x F(x) =0 = a +b ⇒b=−a =−1 F(x) = (1/x) +((−x +c)/(1+x^2 )) we look tbat c=0 ⇒ F(x) = (1/x) −(x/(1+x^2 )) ⇒ ∫_(π/4) ^(4/π) (dx/(x(1+x^2 ))) = ∫_(π/4) ^(4/π) ((1/x) −(x/(1+x^2 )))dx =[ ln(x)−(1/2)ln(1+x^2 )]_(π/4) ^(4/π) =[ln((x/(√(1+x^2 ))))]_(π/4) ^(4/π) = ln( (4/(π(√(1+((16)/π^2 )))))) −ln( (π/(4(√(1+(π^2 /(16))))))) I =(1−(π/4))((π/2) −1) +1 +(4/π) −(π/2) +ln( (4/(π(√(1+((16)/π^2 )))))) −ln( (π/(4(√(1+(π^2 /(16))))))) .](Q33566.png)
| ||
Question and Answers Forum | ||
Question Number 33328 by prof Abdo imad last updated on 14/Apr/18 | ||
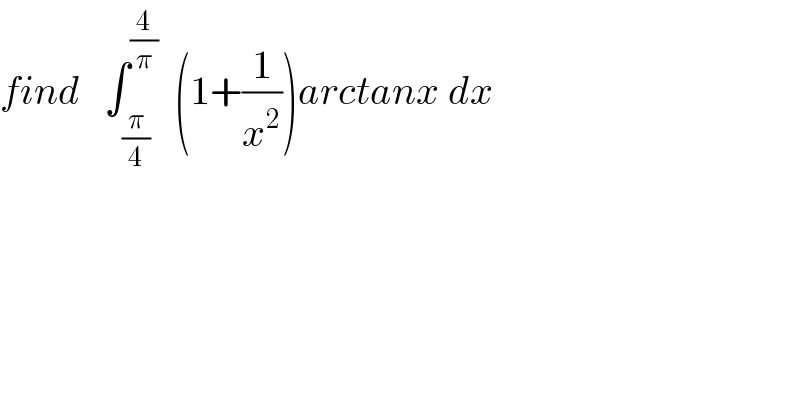 | ||
Commented by math khazana by abdo last updated on 19/Apr/18 | ||
![let put I = ∫_(π/4) ^(4/π) (1+(1/x^2 ))arctanx dx .let integrate by parts u^′ =1+(1/x^2 ) and v =arctanx I = [(1−(1/x))arctanx]_(π/4) ^(4/π) −∫_(π/4) ^(4/π) (1−(1/x)) (dx/(1+x^2 )) = (1−(π/4))arctan((4/π)) −(1−(4/π)) −∫_(π/4) ^(4/π) (dx/(1+x^2 )) + ∫_(π/4) ^(4/π) (dx/(x( 1+x^2 ))) but ∫_(π/4) ^(4/π) (dx/(1+x^2 )) = arctan( (4/π)) −arctan((π/4)) =(π/2) −1−1=(π/2) −2 let?decompose F(x) = (1/(x(1+x^2 ))) = (a/x) +((bx +c)/(1+x^2 )) a =lim_(x→0) x F(x) = 1 lim_(x→+∞) x F(x) =0 = a +b ⇒b=−a =−1 F(x) = (1/x) +((−x +c)/(1+x^2 )) we look tbat c=0 ⇒ F(x) = (1/x) −(x/(1+x^2 )) ⇒ ∫_(π/4) ^(4/π) (dx/(x(1+x^2 ))) = ∫_(π/4) ^(4/π) ((1/x) −(x/(1+x^2 )))dx =[ ln(x)−(1/2)ln(1+x^2 )]_(π/4) ^(4/π) =[ln((x/(√(1+x^2 ))))]_(π/4) ^(4/π) = ln( (4/(π(√(1+((16)/π^2 )))))) −ln( (π/(4(√(1+(π^2 /(16))))))) I =(1−(π/4))((π/2) −1) +1 +(4/π) −(π/2) +ln( (4/(π(√(1+((16)/π^2 )))))) −ln( (π/(4(√(1+(π^2 /(16))))))) .](Q33566.png) | ||