find the area bounded inner the curve r = 4−2cos θ and outer the curve r = 6+2cos θ


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 102369 by bobhans last updated on 08/Jul/20

$f i n d t h e a r e a b o u n d e d i n n e r t h e c u r v e$ $r = 4 - 2 \cos θ a n d o u t e r t h e c u r v e r = 6 + 2 \cos θ$
	Answered by Ar Brandon last updated on 08/Jul/20
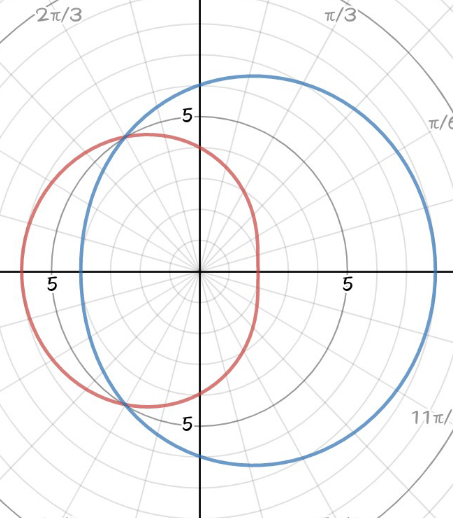
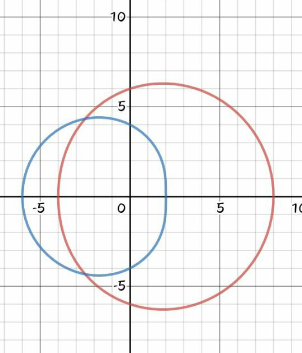
	$Area , A=∫_0 ^(2π) ∫_(4−2cosθ) ^(6+2cosθ) rdrdθ=∫_0 ^(2π) [(r^2 /2)]_(4−2cosθ) ^(6+2cosθ) dθ ⇒A=(1/2)∫_0 ^(2π) {(6+2cosθ)^2 −(4−2cosθ)^2 }dθ =(1/2)∫_0 ^(2π) {(36+24cosθ+4cos^2 θ)−(16−16cosθ+4cos^2 θ)}dθ =(1/2)∫_0 ^(2π) (20+40cosθ)dθ=[((20θ+40sinθ)/2)]_0 ^(2π) =20π square units Don′t really know if I′ve done it in the right way. Please let me know what you think.$
	$Area, A = \int_{0}^{2 π} \int_{4 - 2 \cos θ}^{6 + 2 \cos θ} rdrd θ = \int_{0}^{2 π} {[\frac{r^{2}}{2}]}_{4 - 2 \cos θ}^{6 + 2 \cos θ} d θ$ $\Rightarrow A = \frac{1}{2} \int_{0}^{2 π} {{(6 + 2 \cos θ)}^{2} - {(4 - 2 \cos θ)}^{2}} d θ$ $= \frac{1}{2} \int_{0}^{2 π} {(36 + 24 \cos θ + {4 \cos}^{2} θ) - (16 - 16 \cos θ + {4 \cos}^{2} θ)} d θ$ $= \frac{1}{2} \int_{0}^{2 π} (20 + 40 \cos θ) d θ = {[\frac{20 θ + 40 \sin θ}{2}]}_{0}^{2 π}$ $= 20 π square units$ ${D o n}^{'} t r e a l l y k n o w i f I^{'} v e d o n e i t i n t h e r i g h t w a y .$ $P l e a s e l e t m e k n o w w h a t y o u t h i n k .$
	Commented by mr W last updated on 09/Jul/20

	$y o u a r e r i g h t . i m i s r e a d, b e c a u s e t h i s$ $i s h o w t h e q u e s t i o n i s d i s p l a y e d o n$ $m y d e v i c e :$
	Commented by mr W last updated on 08/Jul/20

	$A = \int_{0}^{2 π} \int_{4 - 2 \cos θ}^{6} rdrd θ$
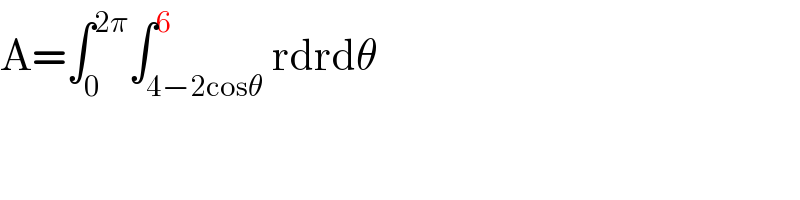
	Commented by Ar Brandon last updated on 08/Jul/20
	Why the 6 at the upper bound, mr W ?
	Commented by mr W last updated on 09/Jul/20

	Commented by mr W last updated on 09/Jul/20

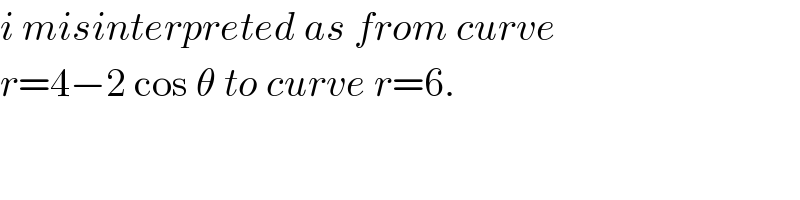
	$i m i s i n t e r p r e t e d a s f r o m c u r v e$ $r = 4 - 2 \cos θ t o c u r v e r = 6 .$
	Commented by bobhans last updated on 09/Jul/20

	$s i r w h y \underset{0}{\int^{2 π}} ? i t h i n k \underset{0}{\int^{π}} ?$
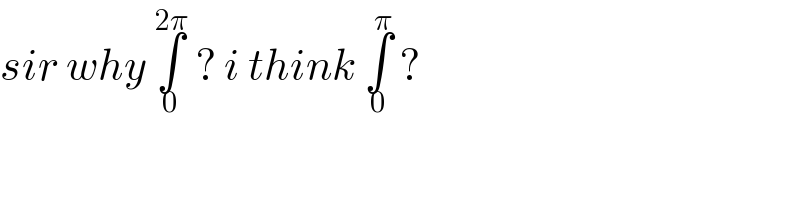
	Commented by bobhans last updated on 09/Jul/20

	Commented by Ar Brandon last updated on 09/Jul/20
	OK Sir
	Commented by Ar Brandon last updated on 09/Jul/20

	${You}^{'} re heading somewhere mr Bobhans . I think {you}^{'} re$ $making a point there . {Let}^{'} s see;$ $Mathematically inner the curve 4 - 2 \cos θ implies$ $4 - 2 \cos θ < r$ $and outer the curve 6 + 2 \cos θ implies$ $6 + 2 \cos θ > r$ $Therefore at points of intersection r = r$ $\Rightarrow 4 - 2 \cos θ = 6 + 2 \cos θ \Rightarrow \cos θ = \frac{- 1}{2}$ $\Rightarrow θ_{1} = \frac{4}{3} π, θ_{2} = \frac{2}{3} π$
	Commented by Ar Brandon last updated on 09/Jul/20

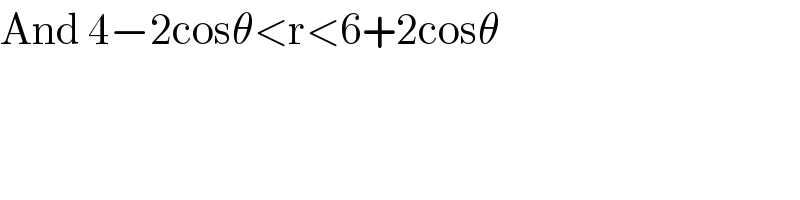
	$And 4 - 2 \cos θ < r < 6 + 2 \cos θ$
	Commented by bemath last updated on 09/Jul/20

	Commented by 1549442205 last updated on 09/Jul/20
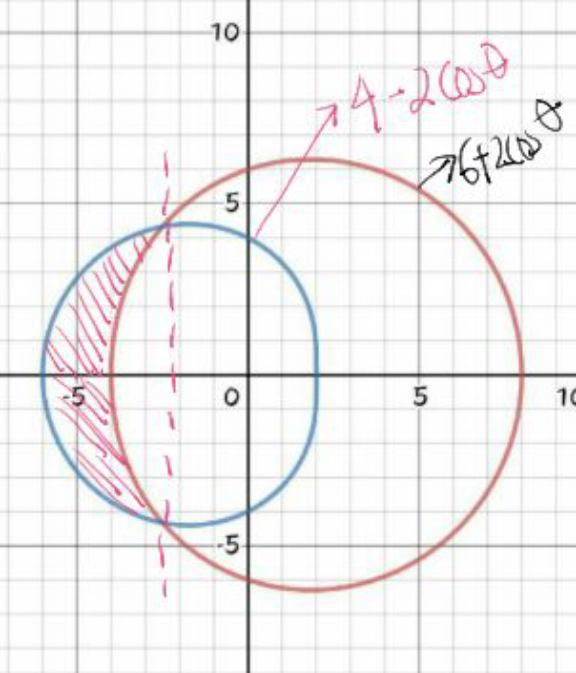
	$If the figure is bounded by { ((r=4−2cosθ)),((r=6)) :} then S=∫_0 ^π [6^2 −(4−2cosθ)^2 ]dθ =∫_0 ^π (20+16cosθ−4cos^2 θ)dθ =(20θ+16sinθ)∣_0 ^π −2∫_0 ^π (1+cos2θ)dθ =20𝛑−(2𝛉+sin2𝛉)∣_0 ^𝛑 =18𝛑 If the figure is bounded { ((r=4−2cosθ)),((r=6+2cosθ)) :}then S=∫_0 ^((2π)/3) [(6+2cosθ)^2 −(4−2cosθ)^2 ]dθ =∫_0 ^((2π)/3) (20+40cosθdθ=(20θ+40sinθ)∣_0 ^((2π)/3) =20×((2𝛑)/3)+40×((√3)/2)=((40𝛑)/3)−20(√(3 )) ≈76.53$
	$If the figure is bounded by$ ${\begin{cases} r = 4 - 2 \cos θ \\ r = 6 \end{cases} then$ $S = \int_{0}^{π} [6^{2} - {(4 - 2 \cos θ)}^{2}] d θ$ $= \int_{0}^{π} (20 + 16 \cos θ - {4 \cos}^{2} θ) d θ$ $= (20 θ + 16 \sin θ) ∣_{0}^{π} - 2 \int_{0}^{π} (1 + \cos 2 θ) d θ$ $= 20 π - (2 θ + \sin 2 θ) ∣_{0}^{π} = 18 π$ $If the figure is bounded {\begin{cases} r = 4 - 2 \cos θ \\ r = 6 + 2 \cos θ \end{cases} then$ $S = \int_{0}^{\frac{2 π}{3}} [{(6 + 2 \cos θ)}^{2} - {(4 - 2 \cos θ)}^{2}] d θ$ $= \int_{0}^{\frac{2 π}{3}} (20 + 40 \cos θ d θ = (20 θ + 40 \sin θ) ∣_{0}^{\frac{2 π}{3}}$ $= 20 \times \frac{2 π}{3} + 40 \times \frac{\sqrt{3}}{2} = \frac{40 π}{3} - 20 \sqrt{3} \approx 76.53$
	Commented by 1549442205 last updated on 09/Jul/20


	Answered by Ar Brandon last updated on 09/Jul/20
	$Area , A=∫_((2π)/3) ^((4π)/3) ∫_(4−2cosθ) ^(6+2cosθ) rdrdθ=∫_((2π)/3) ^((4π)/3) [(r^2 /2)]_(4−2cosθ) ^(6+2cosθ) dθ ⇒A=(1/2)∫_((2π)/3) ^((4π)/3) {(6+2cosθ)^2 −(4−2cosθ)^2 }dθ =(1/2)∫_((2π)/3) ^((4π)/3) {(36+24cosθ+4cos^2 θ)−(16−16cosθ+4cos^2 θ)}dθ =(1/2)∫_((2π)/3) ^((4π)/3) (20+40cosθ)dθ=[((20θ+40sinθ)/2)]_((2π)/3) ^((4π)/3) =(1/2)[20×((4π)/3)−40×((√3)/2)−20×((2π)/3)+40×((√3)/2)] =((20)/3)π square units$
	$Area, A = \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} \int_{4 - 2 \cos θ}^{6 + 2 \cos θ} rdrd θ = \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} {[\frac{r^{2}}{2}]}_{4 - 2 \cos θ}^{6 + 2 \cos θ} d θ$ $\Rightarrow A = \frac{1}{2} \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} {{(6 + 2 \cos θ)}^{2} - {(4 - 2 \cos θ)}^{2}} d θ$ $= \frac{1}{2} \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} {(36 + 24 \cos θ + {4 \cos}^{2} θ) - (16 - 16 \cos θ + {4 \cos}^{2} θ)} d θ$ $= \frac{1}{2} \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} (20 + 40 \cos θ) d θ = {[\frac{20 θ + 40 \sin θ}{2}]}_{\frac{2 π}{3}}^{\frac{4 π}{3}}$ $= \frac{1}{2} [20 \times \frac{4 π}{3} - 40 \times \frac{\sqrt{3}}{2} - 20 \times \frac{2 π}{3} + 40 \times \frac{\sqrt{3}}{2}]$ $= \frac{20}{3} π square units$
	Answered by bemath last updated on 09/Jul/20

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum