Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 89867 by M±th+et£s last updated on 19/Apr/20

$$findtheintegration$$$$\int ln\lfloor x\rfloor dx;x>2$$

Commented by ~blr237~ last updated on 20/Apr/20

Answered by mr W last updated on 20/Apr/20

$$letx=n+f$$$$dx=df$$$$\int \ln \lfloor x\rfloor dx=\ln n\int df=\left(\ln n\right)f+C$$$$=(\ln \lfloor x\rfloor )(x-\lfloor x\rfloor )+C$$

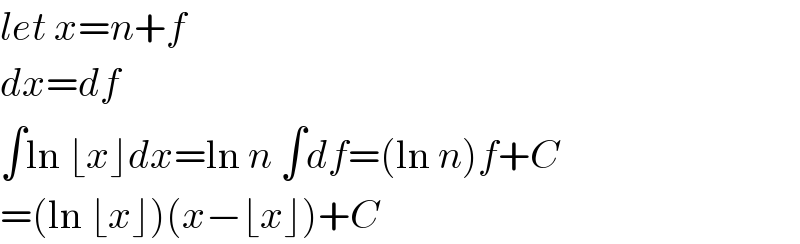
Commented by M±th+et£s last updated on 20/Apr/20

$$sirwhy\int ln\lfloor x\rfloor dx=ln\left(n\right)\int dfandhow$$$$didyougetln(\lfloor x\rfloor )(x-\lfloor x\rfloor )$$

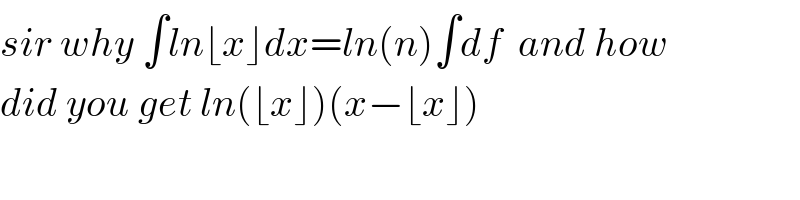
Commented by mr W last updated on 21/Apr/20

$$x=n+fwithn=\lfloor x\rfloor ,f=x-\lfloor x\rfloor$$$$inx=n+f,nisconstant,therefore$$$$dx=df$$$$\int \ln \lfloor x\rfloor dx=\int \left(\ln n\right)df=\ln \left(n\right)\int df$$$$=\ln \left(n\right)f+C$$$$=(\ln \lfloor x\rfloor )(x-\lfloor x\rfloor )+C$$

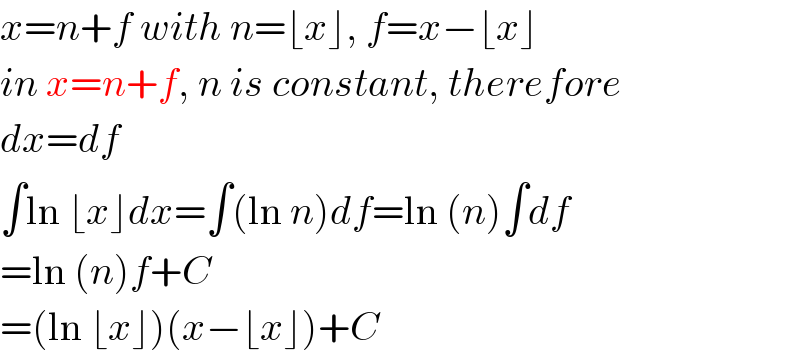
Commented by M±th+et£s last updated on 21/Apr/20

$$thankyouforexplaingthatforme$$

Answered by M±th+et£s last updated on 22/Apr/20

$$itryalotandigetthat$$$$ln\left[x\right]dx=ln\left(2\right)x\in (2,3)$$$$f\left(x\right)=ln\left[x\right]x\in (n,n+1)$$$$\int ln\left[x\right]dx=\underset{k=2}{\sum ^{n-1}}ln\left(x\right)+{\int }_{n=\left[x\right]}^{x}ln\left[x\right]dx$$$$\underset{k=2}{\sum ^{n-1}}ln\left(k\right)+ln\left(n\right)(x-\left[x\right])+c$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com