
Question and Answers Forum
Question Number 32352 by abdo imad last updated on 23/Mar/18
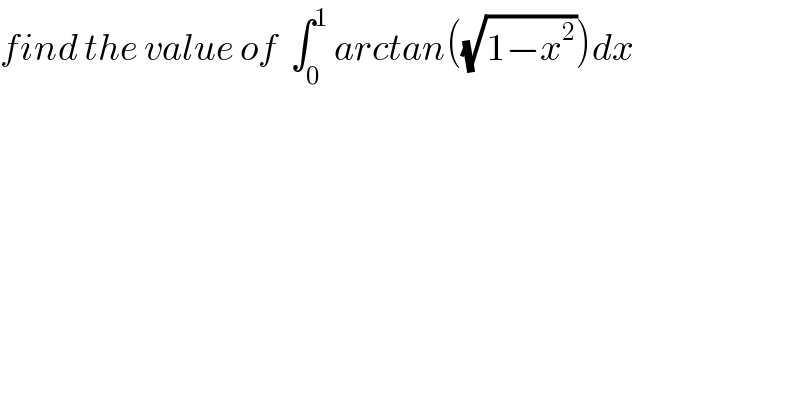
Commented by abdo imad last updated on 26/Mar/18
![ch.x=sint ⇒ I = ∫_0 ^(π/2) arctan(cost) cost dt let integrate by parts u=arctan(cost) and v^′ =cost I = [sint arctan(cost)]_0 ^(π/2) −∫_0 ^(π/2) ((−sint)/(1+cos^2 t)) sint dt = ∫_0 ^(π/2) ((1−cos^2 t)/(1+cos^2 t)) dt = ∫_0 ^(π/2) ((1−((1+cos(2t))/2))/(1 +((1+cos(2t))/2))) dt = ∫_0 ^(π/2) ((1−cos(2t))/(3+cos(2t)))dt =_(2t=u) ∫_0 ^π ((1−cosu)/(3 +cosu)) (du/2) =(1/2) ∫_0 ^π ((1−cosu)/(3 +cosu))du ch.tan((u/2))=x give I = (1/2) ∫_0 ^∞ ((1− ((1−x^2 )/(1+x^2 )))/(3 +((1−x^2 )/(1+x^2 )))) ((2dx)/(1+x^2 )) =∫_0 ^∞ ((1+x^2 −1+x^2 )/((3 +3x^2 +1−x^2 )(1+x^2 ))) dx =∫_0 ^∞ ((2x^2 )/((4+2x^2 )(1+x^2 )))dx = ∫_0 ^∞ (x^2 /((x^2 +1)(x^2 +2)))dx =(1/2) ∫_(−∞) ^(+∞) (x^2 /((x^2 +1)(x^2 +2)))dx let consider ϕ(z) = (z^2 /((z^2 +1)(z^2 +2))) the poles of ϕ are i ,−i, i(√(2 )) ,−i(√2) and all are simples ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ( Res(ϕ,i) +Res(ϕ,i(√2))) ϕ(z) = (z^2 /((z−i)(z+i)(z−i(√2))(z +i(√2)))) Res(ϕ,i) =lim_(z→i) (z−i)ϕ(z)= ((−1)/((2i) (1))) =((−1)/(2i)) Res(ϕ,i(√2)) =lim_(z→i(√2)) (z−i(√2))ϕ(z) = ((−2)/((−1)(2i(√2)))) =(1/(i(√2))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ( ((−1)/(2i)) +(1/(i(√2)))) = −π +((2π)/(√2)) =−π +π(√2) =((√2) −1)π .](Q32514.png)
Commented by abdo imad last updated on 26/Mar/18
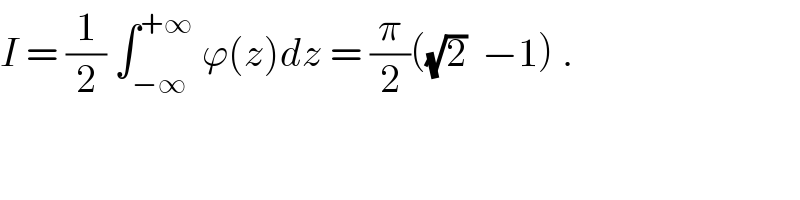
Answered by sma3l2996 last updated on 25/Mar/18
![I=∫_0 ^1 arctan((√(1−x^2 )))dx by parts u=arctan((√(1−x^2 )))⇒u′=((−x)/((2−x^2 )(√(1−x^2 )))) v′=1⇒v=x I=[xarctan((√(1−x^2 )))]_0 ^1 +∫_0 ^1 (x^2 /((2−x^2 )(√(1−x^2 ))))dx =−∫_0 ^1 ((2−x^2 −2)/((2−x^2 )(√(1−x^2 ))))dx=2∫_0 ^1 (dx/((2−x^2 )(√(1−x^2 ))))−∫_0 ^1 (dx/(√(1−x^2 ))) let x=sint⇒dx=costdt I=2∫_0 ^(π/2) (dt/(2−sin^2 t))−(π/2) u=tant⇒dt=(du/(1+u^2 )) 2−sin^2 t=2−((tan^2 t)/(1+tan^2 t))=((2+tan^2 t)/(1+tan^2 t))=((2+u^2 )/(1+u^2 )) I=2∫_0 ^∞ (du/(2+u^2 ))−(π/2)=∫_0 ^∞ (du/(1+((u/(√2)))^2 ))−(π/2)=(√2)[arctan((u/(√2)))]_0 ^∞ −(π/2) I=((π(√2))/2)−(π/2)=(π/2)((√2)−1)](Q32466.png)
| ||
Question and Answers Forum | ||
Question Number 32352 by abdo imad last updated on 23/Mar/18 | ||
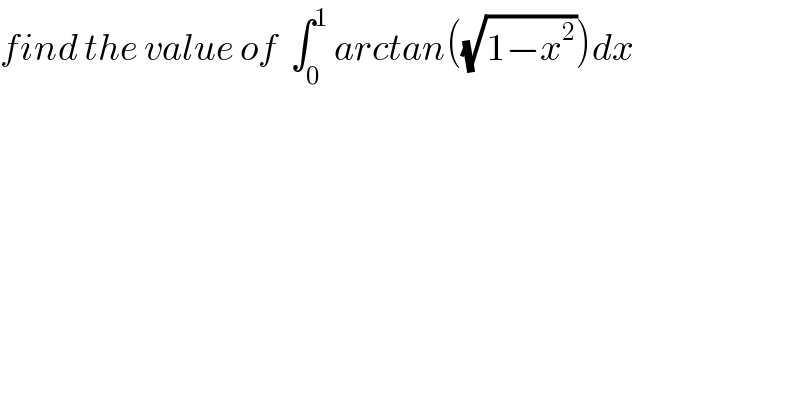 | ||
Commented by abdo imad last updated on 26/Mar/18 | ||
![ch.x=sint ⇒ I = ∫_0 ^(π/2) arctan(cost) cost dt let integrate by parts u=arctan(cost) and v^′ =cost I = [sint arctan(cost)]_0 ^(π/2) −∫_0 ^(π/2) ((−sint)/(1+cos^2 t)) sint dt = ∫_0 ^(π/2) ((1−cos^2 t)/(1+cos^2 t)) dt = ∫_0 ^(π/2) ((1−((1+cos(2t))/2))/(1 +((1+cos(2t))/2))) dt = ∫_0 ^(π/2) ((1−cos(2t))/(3+cos(2t)))dt =_(2t=u) ∫_0 ^π ((1−cosu)/(3 +cosu)) (du/2) =(1/2) ∫_0 ^π ((1−cosu)/(3 +cosu))du ch.tan((u/2))=x give I = (1/2) ∫_0 ^∞ ((1− ((1−x^2 )/(1+x^2 )))/(3 +((1−x^2 )/(1+x^2 )))) ((2dx)/(1+x^2 )) =∫_0 ^∞ ((1+x^2 −1+x^2 )/((3 +3x^2 +1−x^2 )(1+x^2 ))) dx =∫_0 ^∞ ((2x^2 )/((4+2x^2 )(1+x^2 )))dx = ∫_0 ^∞ (x^2 /((x^2 +1)(x^2 +2)))dx =(1/2) ∫_(−∞) ^(+∞) (x^2 /((x^2 +1)(x^2 +2)))dx let consider ϕ(z) = (z^2 /((z^2 +1)(z^2 +2))) the poles of ϕ are i ,−i, i(√(2 )) ,−i(√2) and all are simples ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ( Res(ϕ,i) +Res(ϕ,i(√2))) ϕ(z) = (z^2 /((z−i)(z+i)(z−i(√2))(z +i(√2)))) Res(ϕ,i) =lim_(z→i) (z−i)ϕ(z)= ((−1)/((2i) (1))) =((−1)/(2i)) Res(ϕ,i(√2)) =lim_(z→i(√2)) (z−i(√2))ϕ(z) = ((−2)/((−1)(2i(√2)))) =(1/(i(√2))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ( ((−1)/(2i)) +(1/(i(√2)))) = −π +((2π)/(√2)) =−π +π(√2) =((√2) −1)π .](Q32514.png) | ||
Commented by abdo imad last updated on 26/Mar/18 | ||
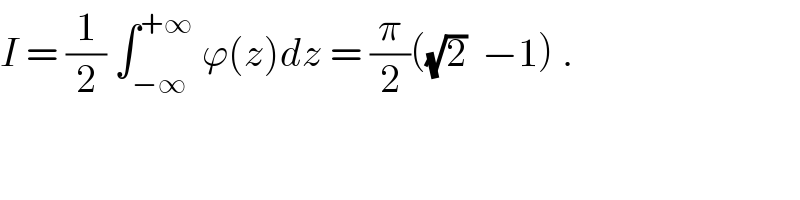 | ||
Answered by sma3l2996 last updated on 25/Mar/18 | ||
![I=∫_0 ^1 arctan((√(1−x^2 )))dx by parts u=arctan((√(1−x^2 )))⇒u′=((−x)/((2−x^2 )(√(1−x^2 )))) v′=1⇒v=x I=[xarctan((√(1−x^2 )))]_0 ^1 +∫_0 ^1 (x^2 /((2−x^2 )(√(1−x^2 ))))dx =−∫_0 ^1 ((2−x^2 −2)/((2−x^2 )(√(1−x^2 ))))dx=2∫_0 ^1 (dx/((2−x^2 )(√(1−x^2 ))))−∫_0 ^1 (dx/(√(1−x^2 ))) let x=sint⇒dx=costdt I=2∫_0 ^(π/2) (dt/(2−sin^2 t))−(π/2) u=tant⇒dt=(du/(1+u^2 )) 2−sin^2 t=2−((tan^2 t)/(1+tan^2 t))=((2+tan^2 t)/(1+tan^2 t))=((2+u^2 )/(1+u^2 )) I=2∫_0 ^∞ (du/(2+u^2 ))−(π/2)=∫_0 ^∞ (du/(1+((u/(√2)))^2 ))−(π/2)=(√2)[arctan((u/(√2)))]_0 ^∞ −(π/2) I=((π(√2))/2)−(π/2)=(π/2)((√2)−1)](Q32466.png) | ||
| ||