
Question and Answers Forum
Question Number 38202 by prof Abdo imad last updated on 22/Jun/18
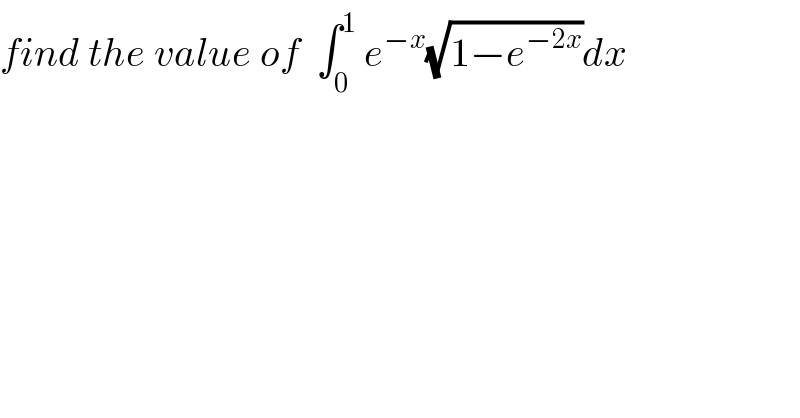
Commented by math khazana by abdo last updated on 23/Jun/18
![changement e^(−x) =t give x=−ln(t) and I =− ∫_1 ^e^(−1) t(√(1−t^2 )) (dt/t) = ∫_(1/e) ^1 (√(1−t^2 ))dt after we use the chang.t=sinθ I = ∫_(arcsin(e^(−1) )) ^(π/2) cosθ.cossθ dθ = ∫_(arcsin(e^(−1) )) ^(π/2) ((1+cos(2θ))/2)dθ =(1/2)( (π/2) −arcsin(e^(−1) )) +(1/4)[sin(2θ)]_(arcsin(e^(−1) )) ^(π/2) =(π/4) −(1/2)arcsin(e^(−1) )−(1/4)sin(2arcsin(e^(−1) )).](Q38298.png)
| ||
Question and Answers Forum | ||
Question Number 38202 by prof Abdo imad last updated on 22/Jun/18 | ||
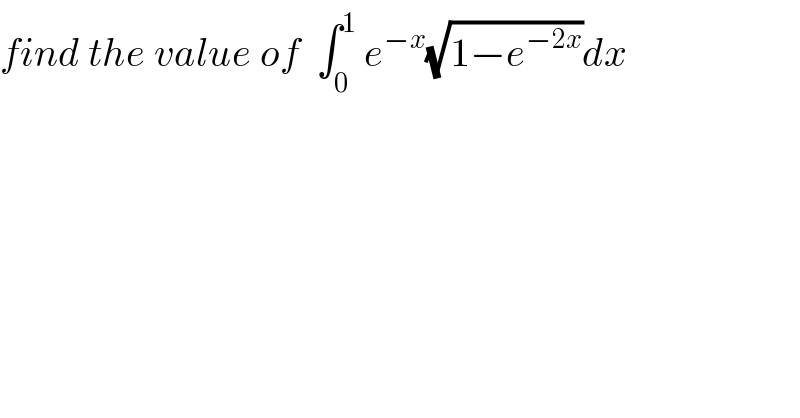 | ||
Commented by math khazana by abdo last updated on 23/Jun/18 | ||
![changement e^(−x) =t give x=−ln(t) and I =− ∫_1 ^e^(−1) t(√(1−t^2 )) (dt/t) = ∫_(1/e) ^1 (√(1−t^2 ))dt after we use the chang.t=sinθ I = ∫_(arcsin(e^(−1) )) ^(π/2) cosθ.cossθ dθ = ∫_(arcsin(e^(−1) )) ^(π/2) ((1+cos(2θ))/2)dθ =(1/2)( (π/2) −arcsin(e^(−1) )) +(1/4)[sin(2θ)]_(arcsin(e^(−1) )) ^(π/2) =(π/4) −(1/2)arcsin(e^(−1) )−(1/4)sin(2arcsin(e^(−1) )).](Q38298.png) | ||