
Question and Answers Forum
Question Number 40154 by maxmathsup by imad last updated on 16/Jul/18
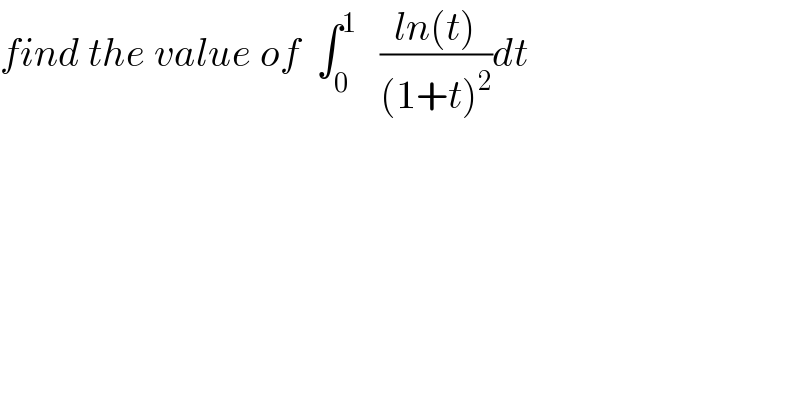
Commented by maxmathsup by imad last updated on 16/Jul/18
![let I = ∫_0 ^1 ((ln(t))/((1+t)^2 ))dt let integrate by parts u^′ =(1/((1+t)^2 )) and v=ln(t) I = [(1−(1/(1+t)))ln(t)]_0 ^1 −∫_0 ^1 (1−(1/(1+t)))(dt/t) = −∫_0 ^1 (dt/(1+t)) =−[ln∣1+t∣]_0 ^1 =−ln(2) I =−ln(2) .](Q40201.png)
Answered by ajfour last updated on 16/Jul/18
![I=∫_0 ^( 1) ((ln t)/((1+t)^2 )) = −((ln t)/((1+t)))∣_0 ^1 +∫_0 ^( 1) (dt/(t(1+t))) = lim_(t→0) [(((ln t)/(1+t)))−ln ((t/(1+t)))]−ln 2 =lim_(t→0) [ln (((1+t)t^(1+t) )/t)]−ln 2 =lim_(t→0) [ln (1+t)t^t ]−ln 2 =lim_(t→0) ln (1+t)+lim_(t→0) ((ln t)/((1/t)))−ln 2 = 0+lim_(t→0) (((1/t)/(−1/t^2 ))) −ln 2 I= −ln 2 .](Q40169.png)
| ||
Question and Answers Forum | ||
Question Number 40154 by maxmathsup by imad last updated on 16/Jul/18 | ||
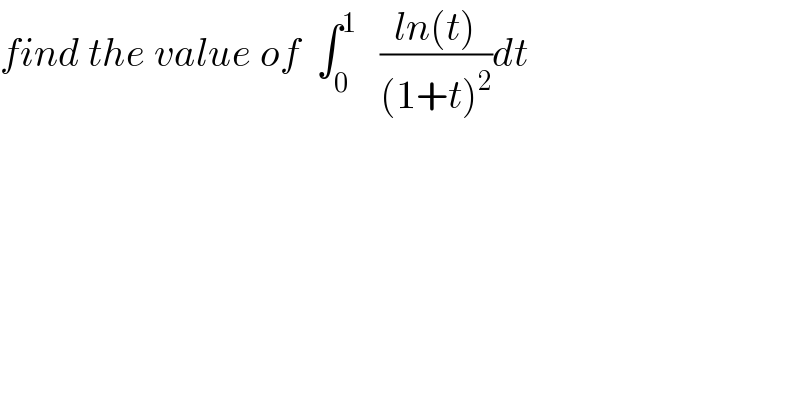 | ||
Commented by maxmathsup by imad last updated on 16/Jul/18 | ||
![let I = ∫_0 ^1 ((ln(t))/((1+t)^2 ))dt let integrate by parts u^′ =(1/((1+t)^2 )) and v=ln(t) I = [(1−(1/(1+t)))ln(t)]_0 ^1 −∫_0 ^1 (1−(1/(1+t)))(dt/t) = −∫_0 ^1 (dt/(1+t)) =−[ln∣1+t∣]_0 ^1 =−ln(2) I =−ln(2) .](Q40201.png) | ||
Answered by ajfour last updated on 16/Jul/18 | ||
![I=∫_0 ^( 1) ((ln t)/((1+t)^2 )) = −((ln t)/((1+t)))∣_0 ^1 +∫_0 ^( 1) (dt/(t(1+t))) = lim_(t→0) [(((ln t)/(1+t)))−ln ((t/(1+t)))]−ln 2 =lim_(t→0) [ln (((1+t)t^(1+t) )/t)]−ln 2 =lim_(t→0) [ln (1+t)t^t ]−ln 2 =lim_(t→0) ln (1+t)+lim_(t→0) ((ln t)/((1/t)))−ln 2 = 0+lim_(t→0) (((1/t)/(−1/t^2 ))) −ln 2 I= −ln 2 .](Q40169.png) | ||
| ||