
Question and Answers Forum
Question Number 67526 by mathmax by abdo last updated on 28/Aug/19
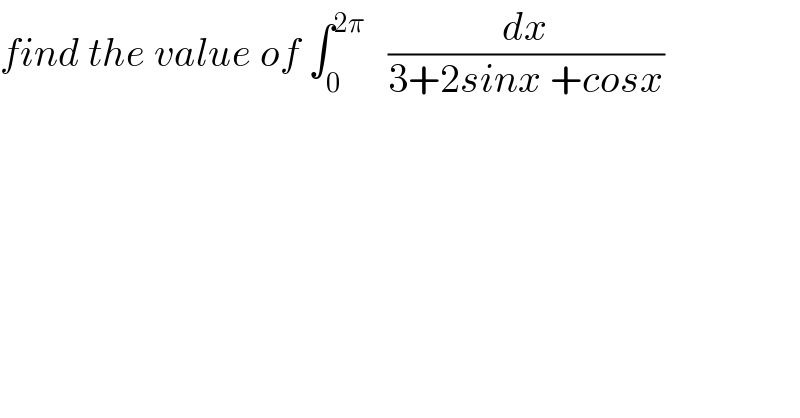
Commented by mathmax by abdo last updated on 31/Aug/19
![let I =∫_0 ^(2π) (dx/(3+2sinx +cosx)) ⇒I =∫_0 ^π (dx/(3+2sinx +cosx)) +∫_π ^(2π) (dx/(3+2sinx +cosx)) =H +K H =_(tan((x/2))=t) ∫_0 ^∞ (1/(3+2((2t)/(1+t^2 )) +((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫_0 ^∞ ((2dt)/(3+3t^2 +4t +1−t^2 )) =∫_0 ^∞ ((2dt)/(2t^2 +4t+4)) =∫_0 ^∞ (dt/(t^2 +2t +2)) Δ^′ =1−2 =−1<0 ⇒ H =∫_0 ^∞ (dt/(t^2 +2t+1 +1)) =∫_0 ^∞ (dt/((t+1)^2 +1)) =_(t+1 =α) ∫_1 ^(+∞) (dα/(1+α^2 )) =[arctan(α)]_1 ^(+∞) =(π/2)−(π/4) =(π/4) K =_(x =π +t) ∫_0 ^π (dt/(3−2sint−cost)) =_(tan((t/2))=u) ∫_0 ^∞ ((2du)/((1+u^2 )(3−2((2u)/(1+u^2 ))−((1−u^2 )/(1+u^2 ))))) =∫_0 ^∞ ((2du)/(3+3u^2 −4u−1+u^2 )) =∫_0 ^∞ ((2du)/(4u^2 −4u+2)) =∫_0 ^∞ (du/(2u^2 −2u +1)) =(1/2)∫_0 ^∞ (du/(u^2 −u +(1/2))) =(1/2)∫_0 ^∞ (du/((u−(1/2))^2 +(3/4)+(1/2))) =(1/2)∫_0 ^∞ (du/((u−(1/2))^2 +(5/4))) =_(u−(1/2)=((√5)/2)α) (1/2)×(4/5)∫_(−(1/(√5))) ^(+∞) (1/(1+u^2 ))((√5)/2)dα =(1/(√5))[arctanα]_(−(1/(√5))) ^(+∞) =(1/(√5)){(π/2) +arctan((1/(√5)))} ⇒ I =(π/4) +(π/(2(√5))) +(1/(√5)) arctan((1/(√5))).](Q67802.png)
| ||
Question and Answers Forum | ||
Question Number 67526 by mathmax by abdo last updated on 28/Aug/19 | ||
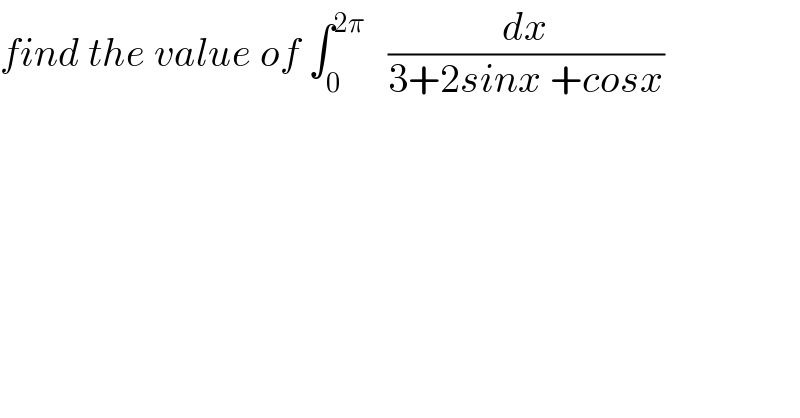 | ||
Commented by mathmax by abdo last updated on 31/Aug/19 | ||
![let I =∫_0 ^(2π) (dx/(3+2sinx +cosx)) ⇒I =∫_0 ^π (dx/(3+2sinx +cosx)) +∫_π ^(2π) (dx/(3+2sinx +cosx)) =H +K H =_(tan((x/2))=t) ∫_0 ^∞ (1/(3+2((2t)/(1+t^2 )) +((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫_0 ^∞ ((2dt)/(3+3t^2 +4t +1−t^2 )) =∫_0 ^∞ ((2dt)/(2t^2 +4t+4)) =∫_0 ^∞ (dt/(t^2 +2t +2)) Δ^′ =1−2 =−1<0 ⇒ H =∫_0 ^∞ (dt/(t^2 +2t+1 +1)) =∫_0 ^∞ (dt/((t+1)^2 +1)) =_(t+1 =α) ∫_1 ^(+∞) (dα/(1+α^2 )) =[arctan(α)]_1 ^(+∞) =(π/2)−(π/4) =(π/4) K =_(x =π +t) ∫_0 ^π (dt/(3−2sint−cost)) =_(tan((t/2))=u) ∫_0 ^∞ ((2du)/((1+u^2 )(3−2((2u)/(1+u^2 ))−((1−u^2 )/(1+u^2 ))))) =∫_0 ^∞ ((2du)/(3+3u^2 −4u−1+u^2 )) =∫_0 ^∞ ((2du)/(4u^2 −4u+2)) =∫_0 ^∞ (du/(2u^2 −2u +1)) =(1/2)∫_0 ^∞ (du/(u^2 −u +(1/2))) =(1/2)∫_0 ^∞ (du/((u−(1/2))^2 +(3/4)+(1/2))) =(1/2)∫_0 ^∞ (du/((u−(1/2))^2 +(5/4))) =_(u−(1/2)=((√5)/2)α) (1/2)×(4/5)∫_(−(1/(√5))) ^(+∞) (1/(1+u^2 ))((√5)/2)dα =(1/(√5))[arctanα]_(−(1/(√5))) ^(+∞) =(1/(√5)){(π/2) +arctan((1/(√5)))} ⇒ I =(π/4) +(π/(2(√5))) +(1/(√5)) arctan((1/(√5))).](Q67802.png) | ||