
Question and Answers Forum
Question Number 65768 by mathmax by abdo last updated on 03/Aug/19
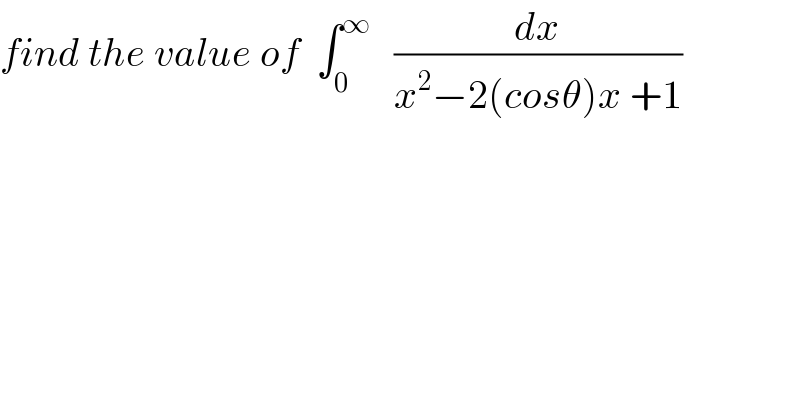
Commented by mathmax by abdo last updated on 04/Aug/19
![let I =∫_0 ^∞ (dx/(x^2 −2xcosθ +1)) ⇒I =∫_0 ^∞ (dx/(x^2 −2xcosθ +cos^2 θ +sin^2 θ)) =∫_0 ^∞ (dx/((x−cosθ)^2 +sin^2 θ)) =_(x−cosθ =∣sinθ∣u) ∫_(−((cosθ)/(∣sinθ∣))) ^(+∞) ((∣sinθ∣du)/(sin^2 θ(1+u^2 ))) =(1/(∣sinθ∣))[arctanu]_(−((cosθ)/(∣sinθ∣))) ^(+∞) =(1/(∣sinθ∣)){(π/2) +arctan(((cosθ)/(∣sinθ∣)))} case 1 sinθ>0 ⇒I =(1/(sinθ)){(π/2) +arctan((1/(tanθ)))} =(1/(sinθ)){ (π/2) +^− (π/2) −θ} case 2 sinθ<0 ⇒ I =−(1/(sinθ)){(π/2) −arctan(((cosθ)/(snθ)))} =(1/(sinθ)){−(π/2) +^− (π/2) −θ}](Q65818.png)
| ||
Question and Answers Forum | ||
Question Number 65768 by mathmax by abdo last updated on 03/Aug/19 | ||
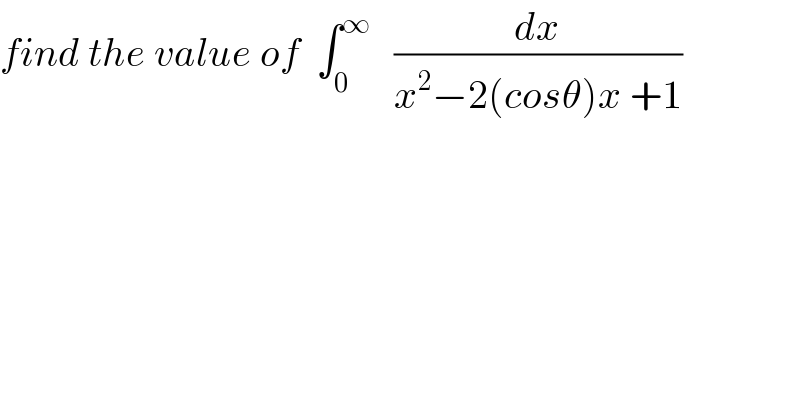 | ||
Commented by mathmax by abdo last updated on 04/Aug/19 | ||
![let I =∫_0 ^∞ (dx/(x^2 −2xcosθ +1)) ⇒I =∫_0 ^∞ (dx/(x^2 −2xcosθ +cos^2 θ +sin^2 θ)) =∫_0 ^∞ (dx/((x−cosθ)^2 +sin^2 θ)) =_(x−cosθ =∣sinθ∣u) ∫_(−((cosθ)/(∣sinθ∣))) ^(+∞) ((∣sinθ∣du)/(sin^2 θ(1+u^2 ))) =(1/(∣sinθ∣))[arctanu]_(−((cosθ)/(∣sinθ∣))) ^(+∞) =(1/(∣sinθ∣)){(π/2) +arctan(((cosθ)/(∣sinθ∣)))} case 1 sinθ>0 ⇒I =(1/(sinθ)){(π/2) +arctan((1/(tanθ)))} =(1/(sinθ)){ (π/2) +^− (π/2) −θ} case 2 sinθ<0 ⇒ I =−(1/(sinθ)){(π/2) −arctan(((cosθ)/(snθ)))} =(1/(sinθ)){−(π/2) +^− (π/2) −θ}](Q65818.png) | ||