Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 65769 by mathmax by abdo last updated on 03/Aug/19

$$findthevalueof{\int }_0^{\mathrm{\infty }}\frac{dx}{{(x^2-2xcos\theta +1)}^2}$$

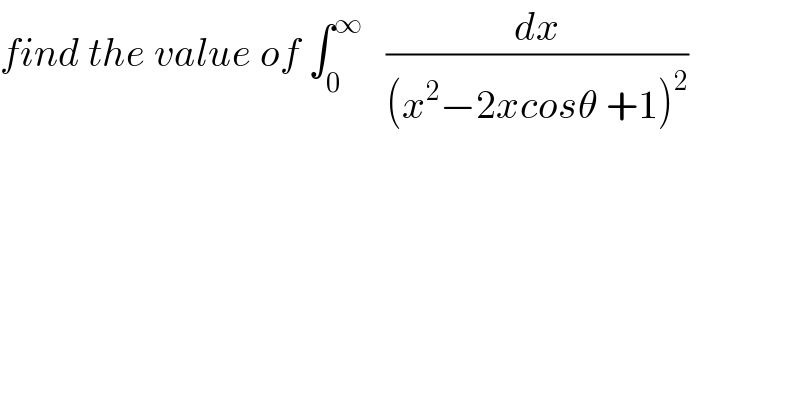
Commented by ~ À ® @ 237 ~ last updated on 04/Aug/19

$$LetsnamedIthevaluewearesearching.Andf\left(x\right)=\frac{1}{{(x^2-2xcos\theta +1)}^2}$$$$x^2-2xcos\theta +1=(x-e^{i\theta })(x-e^{-i\theta })$$$$Im\left(e^{i\theta }\right)=sin\theta >0\Rightarrow \theta \in D=\underset{k=0}{\cup }]2k\pi (2k+1)\pi [etIm\left(e^{-i\theta }\right)<0$$$$Im\left(e^{-i\theta }\right)=-sin\theta >0\Rightarrow \theta \notin D$$$$if\theta \in Dwewillhavesin\theta >0$$$$SoI=2i\pi Res(f.e^{i\theta })$$$$AndRes(f.e^{i\theta })={lim}_{z->e^{i\theta }}\frac{1}{(2-1)!}{\left[\frac{1}{{(z-e^{-i\theta })}^2}\right]}^{\left(1\right)}=\frac{-2}{{(e^{i\theta }-e^{-i\theta })}^3}=\frac{-i}{4{\left(sin\theta \right)}^3}$$$$ThenI=\frac{\pi }{2{sin}^3\left(\theta \right)}$$$$if\theta \notin Dthensin\theta <0$$$$soI=2i\pi Res(f.e^{-i\theta })$$$$andRes(f.e^{-i\theta })={lim}_{z->e^{-i\theta }}\frac{1}{(2-1)!}{\left[\frac{1}{{(z-e^{i\theta })}^2}\right]}^{\left(1\right)}=\frac{-2}{{(e^{-i\theta }-e^{i\theta })}^3}=\frac{i}{4{sin}^3\theta }$$$$thenI=\frac{-\pi }{2{sin}^3\left(\theta \right)}$$$$FinallywecanconcludethatI=\frac{\pi }{2\mid sin\theta {\mid }^3}$$

Commented by mathmax by abdo last updated on 04/Aug/19

$$thankyousir$$

Commented by mathmax by abdo last updated on 04/Aug/19

$$letf\left(a\right)={\int }_0^{\mathrm{\infty }}\frac{dx}{x^2-2xcos\theta +a}witha>{cos}^2\theta$$$$wehave{f}^{{}^{\prime }}\left(a\right)=-{\int }_0^{\mathrm{\infty }}\frac{dx}{{(x^2-2xcos\theta +a)}^2}\Rightarrow$$$${\int }_0^{\mathrm{\infty }}\frac{dx}{{(x^2-2xcos\theta +1)}^2}=-f^{{}^{\prime }}\left(1\right)letfirstfindf\left(a\right)$$$$f\left(a\right)={\int }_0^{\mathrm{\infty }}\frac{dx}{x^2-2xcos\theta +{cos}^2\theta +a-{cos}^2\theta }$$$$={\int }_0^{\mathrm{\infty }}\frac{dx}{{(x-cos\theta )}^2+a-{cos}^2\theta }changementx-cos\theta =\sqrt{a-{cos}^2\theta }u$$$$givef\left(a\right)={\int }_0^{\mathrm{\infty }}\frac{\sqrt{a-{cos}^2\theta }du}{(a-{cos}^2\theta )(1+u^2)}=\frac{1}{\sqrt{a-{cos}^2\theta }}\frac{\pi }{2}=\frac{\pi }{2\sqrt{a-{cos}^2\theta }}$$$${\Rightarrow f^{{}^{\prime }}\left(a\right)=\frac{\pi }{2}{(a-{cos}^2\theta )}^{-\frac{1}{2}}\}}^{\left(1\right)}=-\frac{\pi }{4}{(a-{cos}^2\theta )}^{-\frac{3}{2}}$$$$=-\frac{\pi }{4(a-{cos}^2\theta )\sqrt{a-{cos}^2\theta }}\Rightarrow f^{{}^{\prime }}\left(1\right)=\frac{\pi }{4(1-{cos}^2\theta )\sqrt{1-{cos}^2\theta }}$$$$=\frac{\pi }{4{sin}^2\theta \mid sin\theta \mid }\Rightarrow$$$${\int }_0^{\mathrm{\infty }}\frac{dx}{{(x^2-2xcos\theta +1)}^2}=\frac{\pi }{4\mid sin\theta {\mid }^3}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com