
Question and Answers Forum
Question Number 40143 by maxmathsup by imad last updated on 16/Jul/18
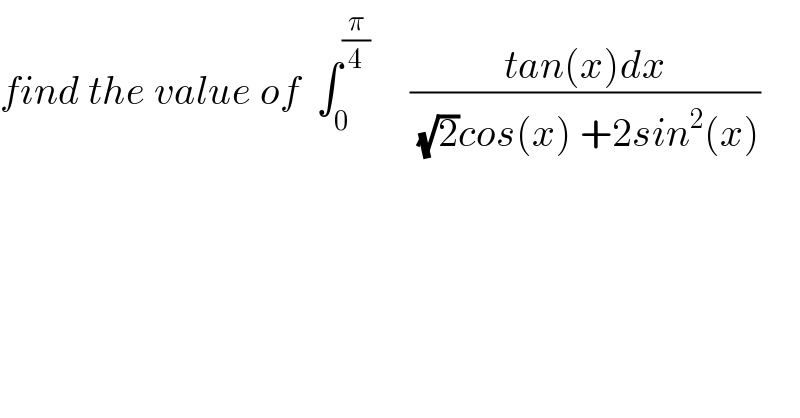
Commented by math khazana by abdo last updated on 22/Jul/18
![I = ∫_0 ^(π/4) ((sinx)/(cosx((√2)cosx +2(1−cos^2 x)))dx changement cosx =t give I = ∫_1 ^(1/(√2)) ((√(1−t^2 ))/(t{(√2)t +2−2t^2 })) ((−dt)/(√(1−t^2 ))) = ∫_(1/(√2)) ^1 (dt/(t{−2t^2 +(√2)t +2})) let decompose F(t) = (1/(t{ −2t^2 +(√2) t+2})) Δ^ =2−4(−2)2=2 +16 =18 ⇒ t_1 =((−(√2) +3(√2))/(−2)) =(((√2) −3(√2))/2)=−(√2) t_2 =((−(√2) −3(√2))/(−2)) =(((√2)+3(√2))/2)=2(√2) F(t) = (1/(−2t(t−t_1 )(t−t_2 ))) =(a/t) +(b/(t−t_1 )) +(c/(t−t_2 )) a=lim_(t→0) tF(t)=(1/2) b =lim_(t→t_1 ) (t−t_1 )F(t) = ((−1)/(2t_1 (t_1 −t_2 ))) = ((−1)/(−2(√2)(−3(√2)))) = (1/(12)) c = lim_(t→t_2 ) (t−t_2 )F(t)= ((−1)/(2t_2 (t_2 −t_1 ))) =((−1)/(4(√2)(3(√2)))) =((−1)/(24)) ⇒ F(t) = (1/(2t)) +(1/(12(t−t_1 ))) −(1/(24(t−t_2 ))) ⇒ ∫_(1/(√2)) ^1 F(t)dt =(1/2) ∫_(1/(√2)) ^1 (dt/t) +(1/(12)) ∫_(1/(√2)) ^1 (dt/(t+(√2))) −(1/(24)) ∫_(1/(√2)) ^1 (dt/(t−2(√2))) =(1/2)[ln∣t∣]_(1/(√2)) ^1 +(1/(12))[ln∣t+(√2)∣]_(1/(√2)) ^1 −(1/(24))[ln∣t−2(√2)∣]_(1/(√2)) ^1 =((ln((√(2))))/2) +(1/(12)){ln(1+(√2))−ln((√2) +(1/(√2)))} −(1/(24)){ln(2(√2) −1)−ln(2(√2) −(1/(√2)))} .](Q40458.png)
| ||
Question and Answers Forum | ||
Question Number 40143 by maxmathsup by imad last updated on 16/Jul/18 | ||
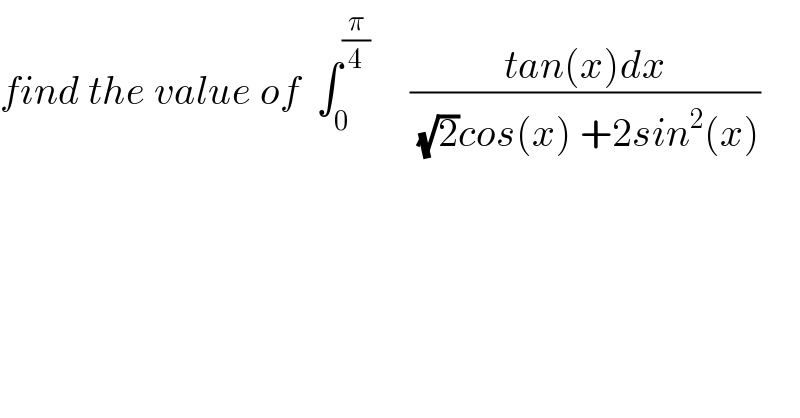 | ||
Commented by math khazana by abdo last updated on 22/Jul/18 | ||
![I = ∫_0 ^(π/4) ((sinx)/(cosx((√2)cosx +2(1−cos^2 x)))dx changement cosx =t give I = ∫_1 ^(1/(√2)) ((√(1−t^2 ))/(t{(√2)t +2−2t^2 })) ((−dt)/(√(1−t^2 ))) = ∫_(1/(√2)) ^1 (dt/(t{−2t^2 +(√2)t +2})) let decompose F(t) = (1/(t{ −2t^2 +(√2) t+2})) Δ^ =2−4(−2)2=2 +16 =18 ⇒ t_1 =((−(√2) +3(√2))/(−2)) =(((√2) −3(√2))/2)=−(√2) t_2 =((−(√2) −3(√2))/(−2)) =(((√2)+3(√2))/2)=2(√2) F(t) = (1/(−2t(t−t_1 )(t−t_2 ))) =(a/t) +(b/(t−t_1 )) +(c/(t−t_2 )) a=lim_(t→0) tF(t)=(1/2) b =lim_(t→t_1 ) (t−t_1 )F(t) = ((−1)/(2t_1 (t_1 −t_2 ))) = ((−1)/(−2(√2)(−3(√2)))) = (1/(12)) c = lim_(t→t_2 ) (t−t_2 )F(t)= ((−1)/(2t_2 (t_2 −t_1 ))) =((−1)/(4(√2)(3(√2)))) =((−1)/(24)) ⇒ F(t) = (1/(2t)) +(1/(12(t−t_1 ))) −(1/(24(t−t_2 ))) ⇒ ∫_(1/(√2)) ^1 F(t)dt =(1/2) ∫_(1/(√2)) ^1 (dt/t) +(1/(12)) ∫_(1/(√2)) ^1 (dt/(t+(√2))) −(1/(24)) ∫_(1/(√2)) ^1 (dt/(t−2(√2))) =(1/2)[ln∣t∣]_(1/(√2)) ^1 +(1/(12))[ln∣t+(√2)∣]_(1/(√2)) ^1 −(1/(24))[ln∣t−2(√2)∣]_(1/(√2)) ^1 =((ln((√(2))))/2) +(1/(12)){ln(1+(√2))−ln((√2) +(1/(√2)))} −(1/(24)){ln(2(√2) −1)−ln(2(√2) −(1/(√2)))} .](Q40458.png) | ||