
Question and Answers Forum
Question Number 27781 by abdo imad last updated on 14/Jan/18
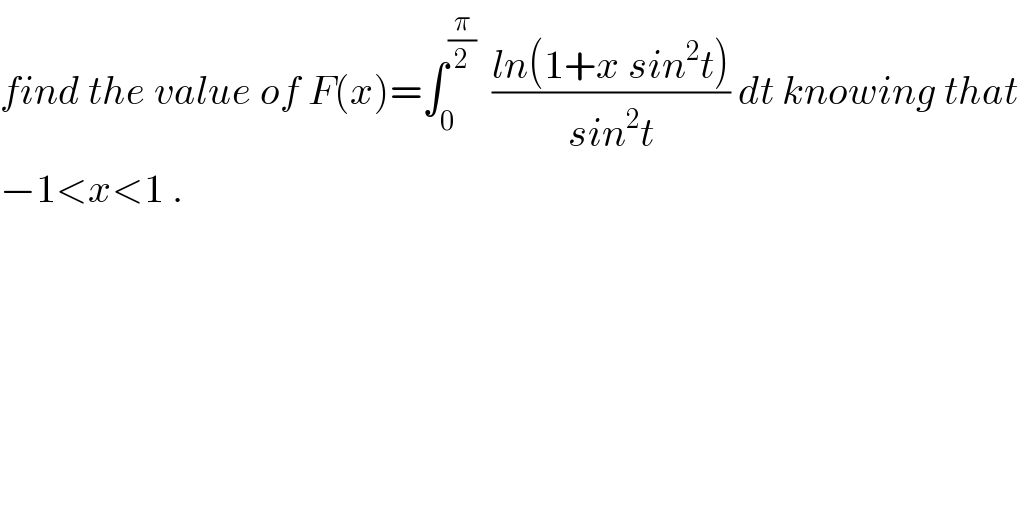
Commented by abdo imad last updated on 18/Jan/18
![after verifying that F is derivable on ]−1,1[ F^(,′) (x)= ∫_0 ^(π/2) ((sin^2 t)/(sin^2 t(1+x sin^2 t)))dt = ∫_0 ^(π/(2 )) (dt/(1+x sin^2 t))= ∫_0 ^(π/2) (dt/(1+x ((1−cos(2t))/2))) = ∫_0 ^(π/2) ((2dt)/(2 +x −x cos(2t))) let use the ch. 2t=θ F^ (x)= ∫_0 ^π (dθ/(2+x −x cosθ)) then the ch. tan((θ/2))=t give F^ (x)= ∫_0 ^(+∝) (1/(2+x −x ((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = ∫_0 ^(+∝) ((2dt)/((2+x)(1+t^2 ) −x +xt^2 )) = ∫_0 ^(+∝) ((2dt)/(2+x +(2+2x)t^2 −x))= ∫_0 ^(+∝) (dt/(1+(1+x)t^2 )) ch. u=(√(1+x))t = ∫_0 ^(+∝) (du/((√(1+x))( 1+u^2 ))) = (π/(2(√(1+x)))) ⇒ F(x)= (π/2) ∫_0 ^x (dt/(√(1+t))) +λ F(x)= π(√(1+x)) +λ and λ = F(0)−π =−π so F(x)= π( (√(1+x)) −1) .](Q28037.png)
| ||
Question and Answers Forum | ||
Question Number 27781 by abdo imad last updated on 14/Jan/18 | ||
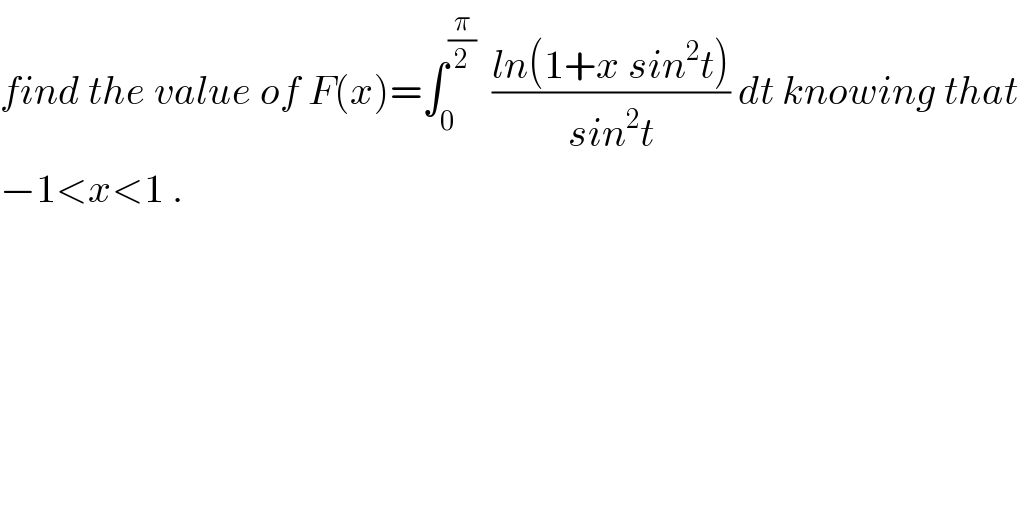 | ||
Commented by abdo imad last updated on 18/Jan/18 | ||
![after verifying that F is derivable on ]−1,1[ F^(,′) (x)= ∫_0 ^(π/2) ((sin^2 t)/(sin^2 t(1+x sin^2 t)))dt = ∫_0 ^(π/(2 )) (dt/(1+x sin^2 t))= ∫_0 ^(π/2) (dt/(1+x ((1−cos(2t))/2))) = ∫_0 ^(π/2) ((2dt)/(2 +x −x cos(2t))) let use the ch. 2t=θ F^ (x)= ∫_0 ^π (dθ/(2+x −x cosθ)) then the ch. tan((θ/2))=t give F^ (x)= ∫_0 ^(+∝) (1/(2+x −x ((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = ∫_0 ^(+∝) ((2dt)/((2+x)(1+t^2 ) −x +xt^2 )) = ∫_0 ^(+∝) ((2dt)/(2+x +(2+2x)t^2 −x))= ∫_0 ^(+∝) (dt/(1+(1+x)t^2 )) ch. u=(√(1+x))t = ∫_0 ^(+∝) (du/((√(1+x))( 1+u^2 ))) = (π/(2(√(1+x)))) ⇒ F(x)= (π/2) ∫_0 ^x (dt/(√(1+t))) +λ F(x)= π(√(1+x)) +λ and λ = F(0)−π =−π so F(x)= π( (√(1+x)) −1) .](Q28037.png) | ||