
Question and Answers Forum
Question Number 35628 by abdo mathsup 649 cc last updated on 21/May/18
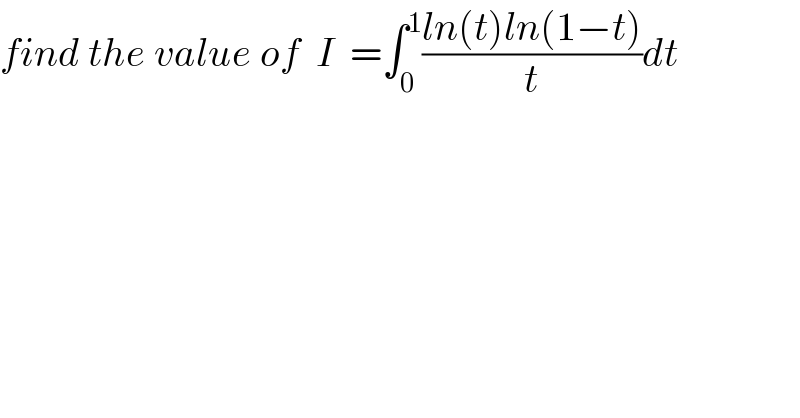
Commented by abdo mathsup 649 cc last updated on 24/May/18
![we have ln^′ (1−t) = ((−1)/(1−t)) =−Σ_(n=0) ^∞ t^n for ∣t∣<1 ⇒ ln(1−t) =−Σ_(n=0) ^∞ (t^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (t^n /n) ⇒ ((ln(1−t))/t) = −Σ_(n=1) ^∞ (t^(n−1) /n) ⇒ I = − ∫_0 ^1 {Σ_(n=1) ^∞ (t^(n−1) /n)}ln(t)dt =−Σ_(n=1) ^∞ (1/n)∫_0 ^1 t^(n−1) ln(t)dt by parts A_n = ∫_0 ^1 t^(n−1) ln(t)dt =[(1/n)t^n ln(t)]_0 ^1 −∫_0 ^1 (1/n)t^n (dt/t) = −(1/n) ∫_0 ^1 t^(n−1) dt = −(1/n^2 ) ⇒ I = Σ_(n=1) ^∞ (1/n^3 ) I =ξ(3) the approximate value of ξ(3) is known.](Q35854.png)
| ||
Question and Answers Forum | ||
Question Number 35628 by abdo mathsup 649 cc last updated on 21/May/18 | ||
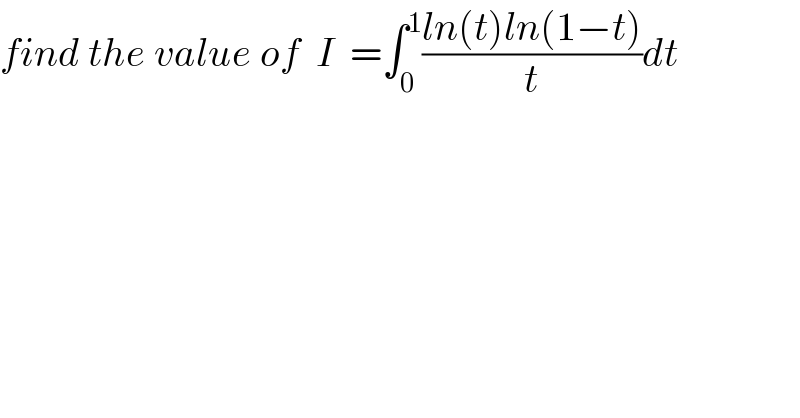 | ||
Commented by abdo mathsup 649 cc last updated on 24/May/18 | ||
![we have ln^′ (1−t) = ((−1)/(1−t)) =−Σ_(n=0) ^∞ t^n for ∣t∣<1 ⇒ ln(1−t) =−Σ_(n=0) ^∞ (t^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (t^n /n) ⇒ ((ln(1−t))/t) = −Σ_(n=1) ^∞ (t^(n−1) /n) ⇒ I = − ∫_0 ^1 {Σ_(n=1) ^∞ (t^(n−1) /n)}ln(t)dt =−Σ_(n=1) ^∞ (1/n)∫_0 ^1 t^(n−1) ln(t)dt by parts A_n = ∫_0 ^1 t^(n−1) ln(t)dt =[(1/n)t^n ln(t)]_0 ^1 −∫_0 ^1 (1/n)t^n (dt/t) = −(1/n) ∫_0 ^1 t^(n−1) dt = −(1/n^2 ) ⇒ I = Σ_(n=1) ^∞ (1/n^3 ) I =ξ(3) the approximate value of ξ(3) is known.](Q35854.png) | ||