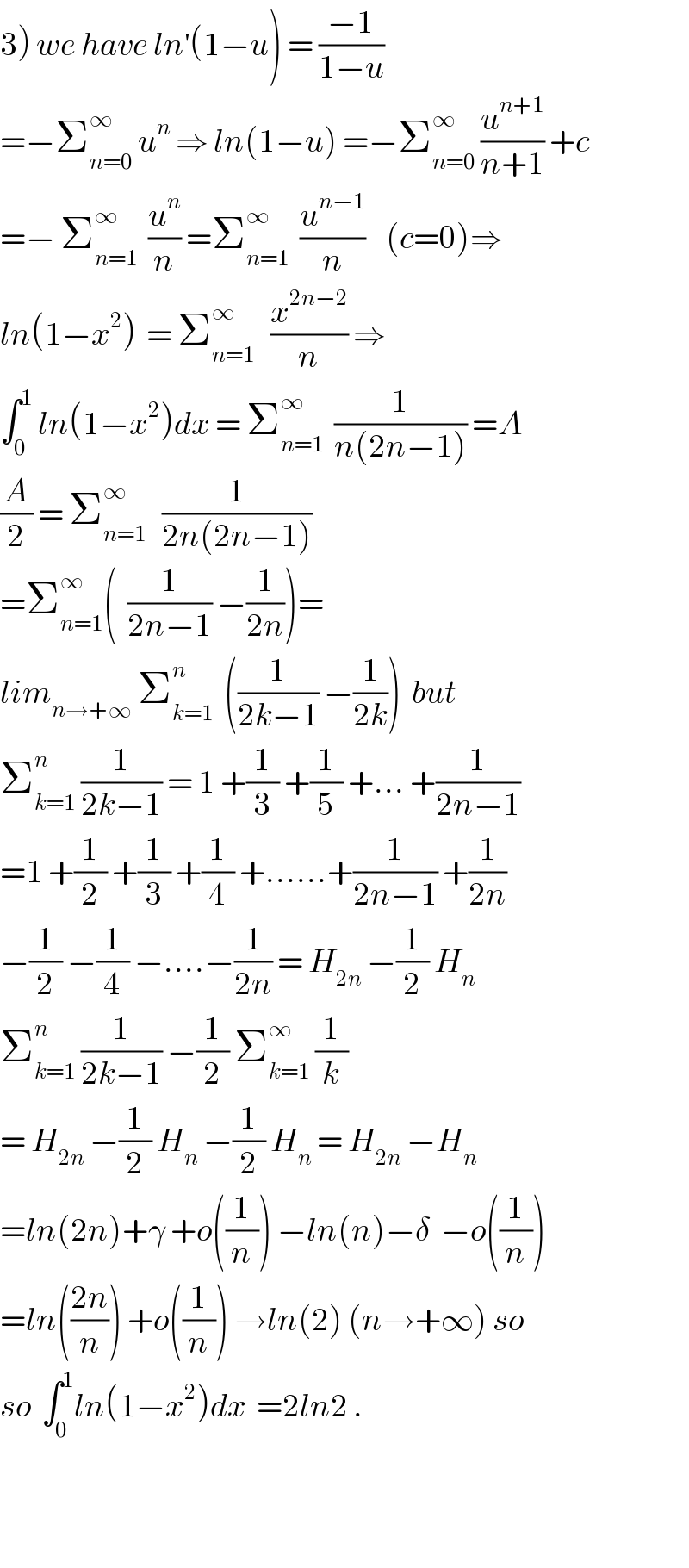Question and Answers Forum
Question Number 36435 by prof Abdo imad last updated on 02/Jun/18
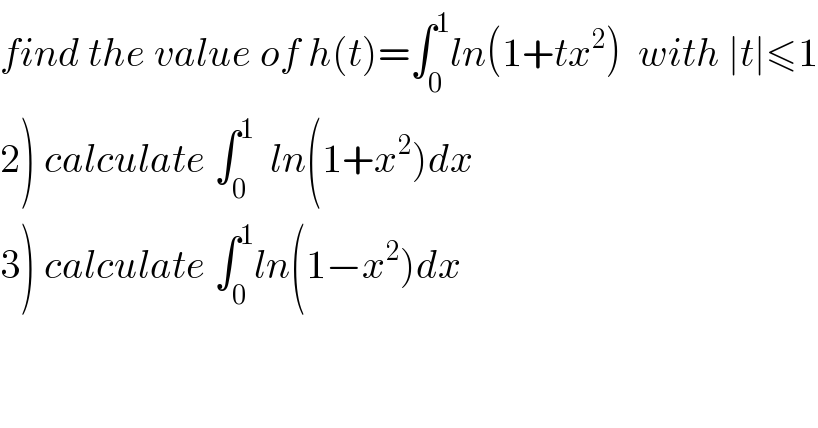
Commented by abdo.msup.com last updated on 03/Jun/18
![another method but easy ∫_0 ^1 ln(1−x^2 )dx = ∫_0 ^1 ln(1−x)dx + ∫_0 ^1 ln(1+x)dx but ∫_0 ^1 ln(1−x)dx =_(1−x=t) −∫_1 ^0 lnt dt = ∫_0 ^1 ln(t)dt = [tln(t)]_0 ^1 =0 ∫_0 ^1 ln(1+x)dx =_(1+x=t) ∫_1 ^2 ln(t)dt =[ tln(t)]_1 ^2 =2ln(2) so ∫_0 ^1 ln(1−x^2 )dx =2ln(2) .](Q36648.png)
Commented by abdo.msup.com last updated on 03/Jun/18
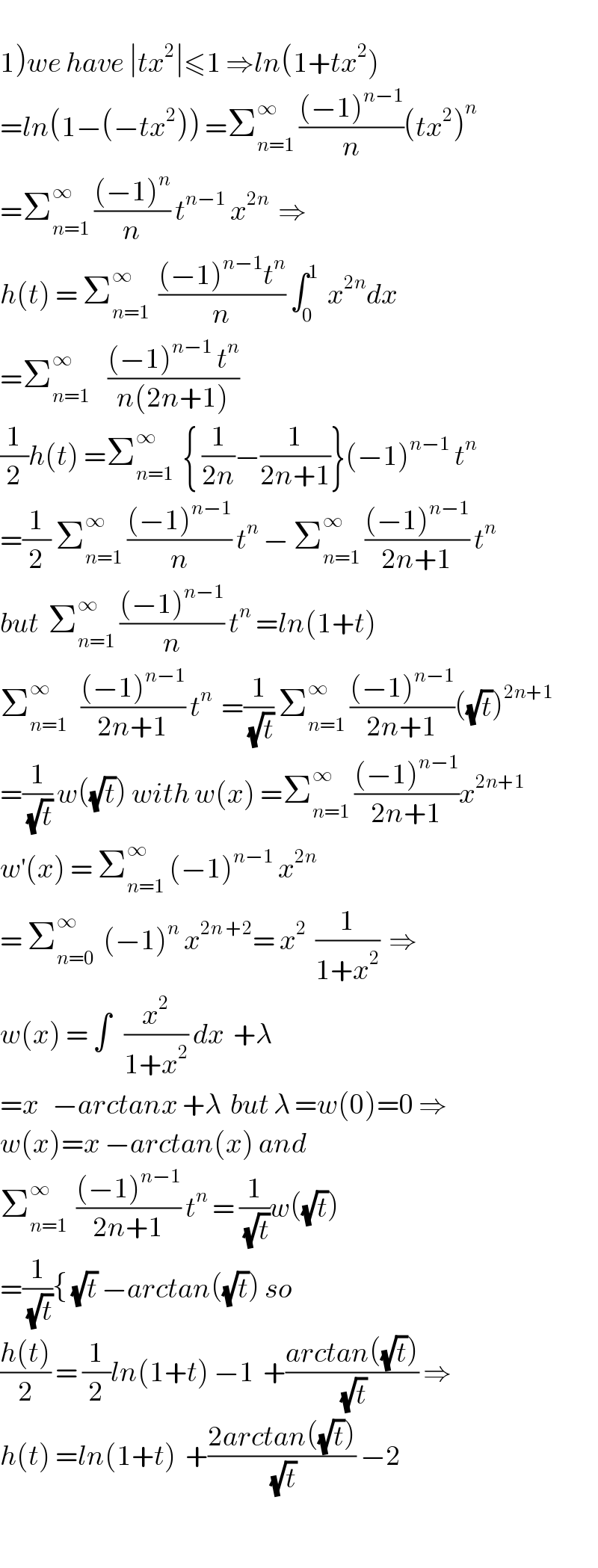
Commented by abdo.msup.com last updated on 03/Jun/18
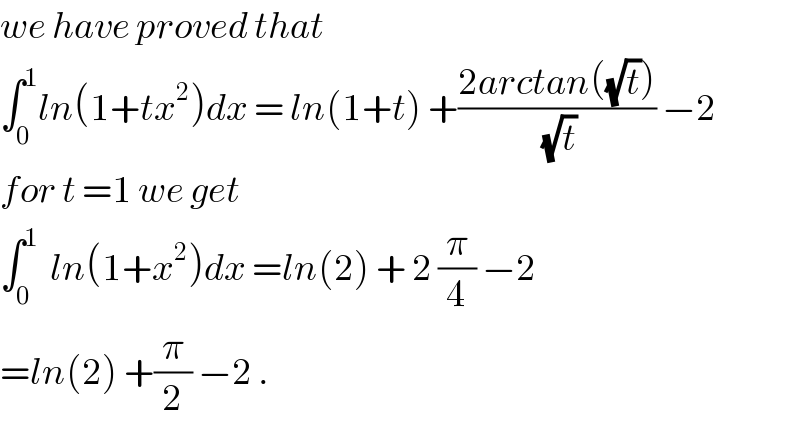
Commented by abdo.msup.com last updated on 03/Jun/18