
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 74351 by mathmax by abdo last updated on 22/Nov/19
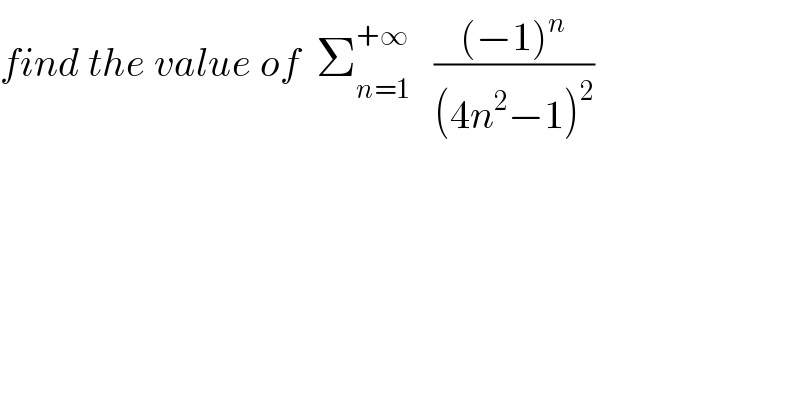
Commented by ~blr237~ last updated on 23/Nov/19
![let named it S S=Σ_(n=1) ^∞ (((−1)^n )/([(2n+1)(2n−1)]^2 )) =Σ_(n=1) ^∞ (((−1)^n )/2)[(((2n+1)−(2n−1))/((2n+1)(2n−1)))]^2 2S=Σ_(n=1) ^∞ (−1)^n [(1/(2n−1))−(1/(2n+1))]^2 2S=Σ_(n=1) ^∞ (−1)^n [(1/((2n−1)^2 ))−(2/((2n+1)(2n−1)))+(1/((2n+1)^2 ))] 2S=Σ_(n=1) ^∞ (((−1)^n )/((2n−1)^2 )) −Σ_(n=1) ^∞ (2/((2n+1)(2n−1)))+Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) 2S=−Σ_(m=0) ^∞ (((−1)^m )/((2m+1)^2 )) −A+Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) with A=Σ_(n=1) ^∞ (2/((2n+1)(2n−1))) 2S=−1−A let state U_n =Σ_(k=1) ^n (2/((2k+1)(2k−1))) we have A=lim_(n→∞) U_n_ U_n =Σ_(k=1) ^n ((1/(2k−1))−(1/(2k+1)))=Σ_(k=0) ^(n−1) (1/(2k+1)) −Σ_(k=1) ^n (1/(2k+1))=1−(1/(2n+1)) So A=1 then S=−2](Q74396.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 74351 by mathmax by abdo last updated on 22/Nov/19 | ||
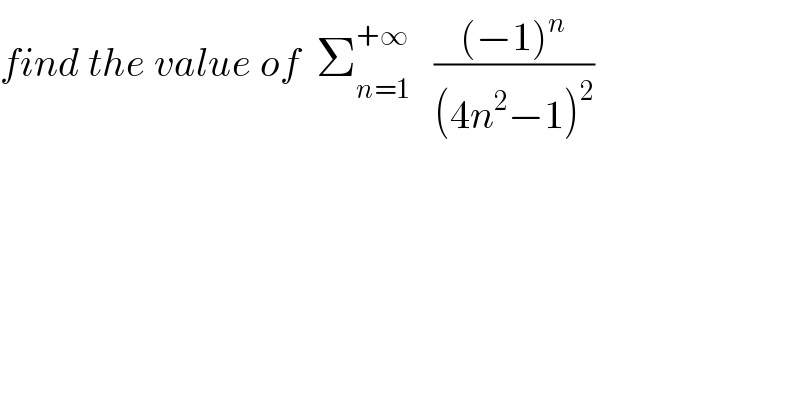 | ||
Commented by ~blr237~ last updated on 23/Nov/19 | ||
![let named it S S=Σ_(n=1) ^∞ (((−1)^n )/([(2n+1)(2n−1)]^2 )) =Σ_(n=1) ^∞ (((−1)^n )/2)[(((2n+1)−(2n−1))/((2n+1)(2n−1)))]^2 2S=Σ_(n=1) ^∞ (−1)^n [(1/(2n−1))−(1/(2n+1))]^2 2S=Σ_(n=1) ^∞ (−1)^n [(1/((2n−1)^2 ))−(2/((2n+1)(2n−1)))+(1/((2n+1)^2 ))] 2S=Σ_(n=1) ^∞ (((−1)^n )/((2n−1)^2 )) −Σ_(n=1) ^∞ (2/((2n+1)(2n−1)))+Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) 2S=−Σ_(m=0) ^∞ (((−1)^m )/((2m+1)^2 )) −A+Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) with A=Σ_(n=1) ^∞ (2/((2n+1)(2n−1))) 2S=−1−A let state U_n =Σ_(k=1) ^n (2/((2k+1)(2k−1))) we have A=lim_(n→∞) U_n_ U_n =Σ_(k=1) ^n ((1/(2k−1))−(1/(2k+1)))=Σ_(k=0) ^(n−1) (1/(2k+1)) −Σ_(k=1) ^n (1/(2k+1))=1−(1/(2n+1)) So A=1 then S=−2](Q74396.png) | ||