find the value of Π_(n=2) ^∞ ((n^3 −1)/(n^3 +1)) and Π


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 67534 by mathmax by abdo last updated on 28/Aug/19

$f i n d t h e v a l u e o f \prod_{n = 2}^{\infty} \frac{n^{3} - 1}{n^{3} + 1}$ $a n d \prod_{n = 1}^{\infty} (1 + \frac{1}{n^{2}})$
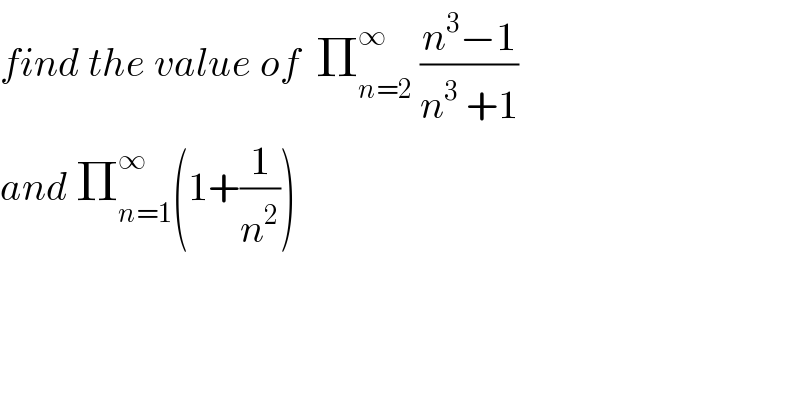
Commented by ~ À ® @ 237 ~ last updated on 29/Aug/19

$A = \underset{n = 2}{\prod^{\infty}} \frac{n^{3} - 1}{n^{3} + 1} = \underset{n = 2}{\prod^{\infty}} \frac{(n - 1) (n^{2} + n + 1)}{(n + 1) (n^{2} - n + 1)}$ $n^{2} + n + 1 = (n - j) (n - \overline{j}) w i t h j = \frac{- 1}{2} + i \frac{\sqrt{3}}{2}$ $n^{2} - n + 1 = {[(n - 1) + 1]}^{2} - (n - 1) = {(n - 1)}^{2} + 2 (n - 1) + 1 - (n - 1) = p^{2} + p + 1 = (p - j) (p - \overline{j}) w i t h p = n - 1$ $n^{2} - n + 1 = (n - 1 - j) (n - 1 - \overline{j})$ $A_{p} = \underset{n = 2}{\prod^{p}} \frac{n - 1}{n + 1} . \underset{n = 2}{\prod^{p}} \frac{(j - n) (\overline{j} - n)}{[j - (n - 1)] [\overline{j} - (n - 1)]} = \frac{(p - 1)!}{\frac{(p + 1)!}{2!}} . \frac{(j - p) (\overline{j} - p)}{(j - 1) (\overline{j} - 1)} = \frac{2}{(2 - 2 R e (j))} . \frac{(j - p) (\overline{j} - p)}{p^{2}}$ $A = \lim_{n \to \infty} A_{p} = \frac{1}{1 - R e (j)} = \frac{2}{3}$ $K n o w i n g t h a t s i n (π z) = π z \underset{n = 1}{\prod^{\infty}} (1 - \frac{z^{2}}{n^{2}}) l e t t a k e z = i a w i t h a \neq 0$ $s i n (i π a) = (i π a) \underset{n = 1}{\prod^{\infty}} (1 + \frac{a^{2}}{n^{2}})$ $\underset{n = 1}{\prod^{\infty}} (1 + \frac{a^{2}}{n^{2}}) = \frac{s i n (i π a)}{i π a} = \frac{\frac{e^{- π a} - e^{π a}}{2 i}}{i π a} = \frac{s h (π a)}{π a}$
Commented by Abdo msup. last updated on 29/Aug/19
$thank you sir. let A =Π_(n=2) ^∞ ((n^3 −1)/(n^3 +1)) and A_n =Π_(k=2) ^n ((k^3 −1)/(k^(3 ) +1)) ⇒ A_n =Π_(k=2) ^n (((k−1)(k^2 +k+1))/((k+1)(k^2 −x+1))) =Π_(k=2) ^n ((k−1)/(k+1))∐_(k=2) ^n ((k^2 +k+1)/(k^2 −k +1)) ⇒ln(A_n )=Σ_(k=2) ^n ln(((k−1)/(k+1)))+Σ_(k=2) ^n ln(((k^2 +k+1)/(k^2 −k+1))) =Σ_(k=2) ^n {ln(k−1)−ln(k+1)) +Σ_(k=2) ^n { ln(k^2 +k+1)−ln(k^2 −k+1)} =Σ_(k=2) ^n {ln(k−1)−ln(k)}+Σ_(k=2) ^n {ln(k)−ln(k+1)} +Σ_(k=2) ^n (u_k −u_(k−1) ) with u_k =ln(k^2 +k+1) =ln(1)−ln(2)+ln(2)−ln(3)+....+ln(n−1)−ln(n) +ln(2)−ln(3)+ln(3)−ln(4)+...+ln(n)−ln(n+1) +u_n −u_1 =−ln(n)+ln(2)−ln(n+1) +ln(n^2 +n+1)−ln(3) =ln((2/3))+ln(((n^2 +n+1)/(n^2 +n)))→ln((2/3)) ⇒lim_(n→+∞) A_n =(2/3)$
$t h a n k y o u s i r .$ $l e t A = \prod_{n = 2}^{\infty} \frac{n^{3} - 1}{n^{3} + 1} a n d A_{n} = \prod_{k = 2}^{n} \frac{k^{3} - 1}{k^{3} + 1} \Rightarrow$ $A_{n} = \prod_{k = 2}^{n} \frac{(k - 1) (k^{2} + k + 1)}{(k + 1) (k^{2} - x + 1)}$ $= \prod_{k = 2}^{n} \frac{k - 1}{k + 1} ∐_{k = 2}^{n} \frac{k^{2} + k + 1}{k^{2} - k + 1}$ $\Rightarrow l n (A_{n}) = \sum_{k = 2}^{n} l n (\frac{k - 1}{k + 1}) + \sum_{k = 2}^{n} l n (\frac{k^{2} + k + 1}{k^{2} - k + 1})$ $= \sum_{k = 2}^{n} {l n (k - 1) - l n (k + 1))$ $+ \sum_{k = 2}^{n} {l n (k^{2} + k + 1) - l n (k^{2} - k + 1)}$ $= \sum_{k = 2}^{n} {l n (k - 1) - l n (k)} + \sum_{k = 2}^{n} {l n (k) - l n (k + 1)}$ $+ \sum_{k = 2}^{n} (u_{k} - u_{k - 1}) w i t h u_{k} = l n (k^{2} + k + 1)$ $= l n (1) - l n (2) + l n (2) - l n (3) + . . . . + l n (n - 1) - l n (n)$ $+ l n (2) - l n (3) + l n (3) - l n (4) + . . . + l n (n) - l n (n + 1)$ $+ u_{n} - u_{1}$ $= - l n (n) + l n (2) - l n (n + 1) + l n (n^{2} + n + 1) - l n (3)$ $= l n (\frac{2}{3}) + l n (\frac{n^{2} + n + 1}{n^{2} + n}) \to l n (\frac{2}{3}) \Rightarrow {l i m}_{n \to + \infty} A_{n} = \frac{2}{3}$
Commented by Abdo msup. last updated on 29/Aug/19

$w e h a v e s i n (π z) = π z \prod_{n = 1}^{\infty} (1 - \frac{z^{2}}{n^{2}})$ $l e t z = i x (x r e a l) \Rightarrow s i n (i π x) = i π x \prod_{n = 1}^{\infty} (1 + \frac{x^{2}}{n^{2}}) \Rightarrow$ $\prod_{n = 1}^{\infty} (1 + \frac{x^{2}}{n^{2}}) = \frac{s i n (i π x)}{i π x}$ $s i n z = \frac{e^{i z} - e^{- i z}}{2 i} \Rightarrow s i n (i π x) = \frac{e^{- π x} - e^{π x}}{2 i}$ $= - \frac{1}{i} s h (π x) \Rightarrow \prod_{n = 1}^{\infty} (1 + \frac{x^{2}}{n^{2}}) = - \frac{1}{i} \frac{s h (π x)}{i π x}$ $= \frac{s h (π x)}{π x}$ $x = 1 \Rightarrow \prod_{n = 1}^{\infty} (1 + \frac{1}{n^{2}}) = \frac{s h (π)}{π} .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum