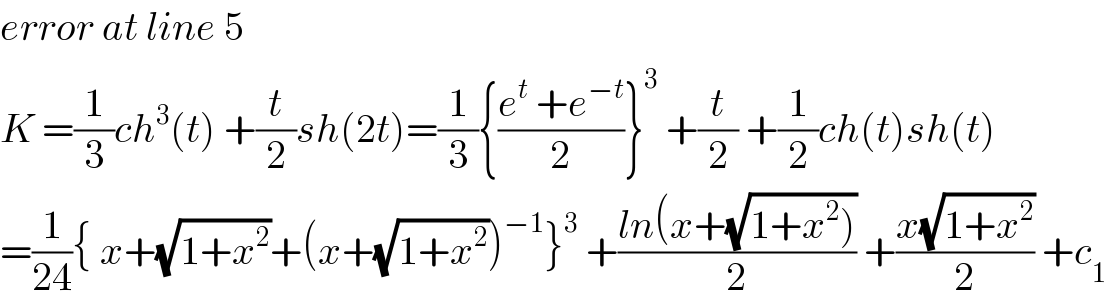find ∫ ((x+1)(√(1+x^2 )) +(1+x^2 )(√(x+1)))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 40620 by math khazana by abdo last updated on 25/Jul/18

$f i n d \int ((x + 1) \sqrt{1 + x^{2}} + (1 + x^{2}) \sqrt{x + 1}) d x$
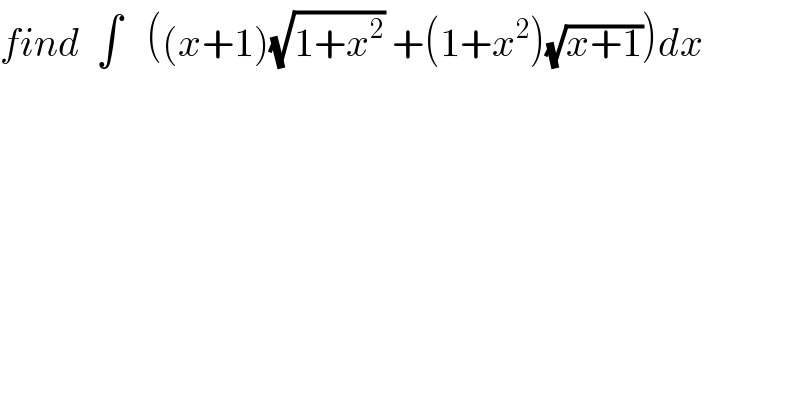
	Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jul/18

	$\int x \sqrt{1 + x^{2}} d x + \int \sqrt{x^{2} + 1} d x + \int \sqrt{x + 1} d x + \int x^{2} \sqrt{x + 1}$ $I_{1} = \int x \sqrt{1 + x^{2}} d x$ $= \frac{1}{2} \int \sqrt{1 + x^{2}} d (1 + x^{2})$ $= \frac{1}{2} \times \frac{2}{3} {(1 + x^{2})}^{\frac{3}{2}}$ $I_{2} = \int \sqrt{x^{2} + 1} d x u s e f o r m u l a$ $= \frac{x}{2} \sqrt{x^{2} + 1} + \frac{1}{2} l n (x + \sqrt{x^{2} + 1})$ $I_{3} = \int \sqrt{x + 1} d x$ $= \frac{{(x + 1)}^{\frac{3}{2}}}{\frac{3}{2}}$ $I_{4} = \int x^{2} \sqrt{x + 1} d x$ $l e t t^{2} = x + 1 2 t d t = d x$ $\int {(t^{2} - 1)}^{2} \times t \times 2 t d t$ $2 \int t^{2} (t^{4} - 2 t^{2} + 1) d t$ $2 \int t^{6} - 2 t^{4} + t^{2} d t$ $2 (\frac{t^{7}}{7} - \frac{2 t^{5}}{5} + \frac{t^{3}}{3})$ $\frac{2}{7} \frac{t^{8}}{8} - \frac{4}{5} \times \frac{t^{6}}{6} + \frac{2}{3} \times \frac{t^{4}}{4}$ $\frac{}{}$
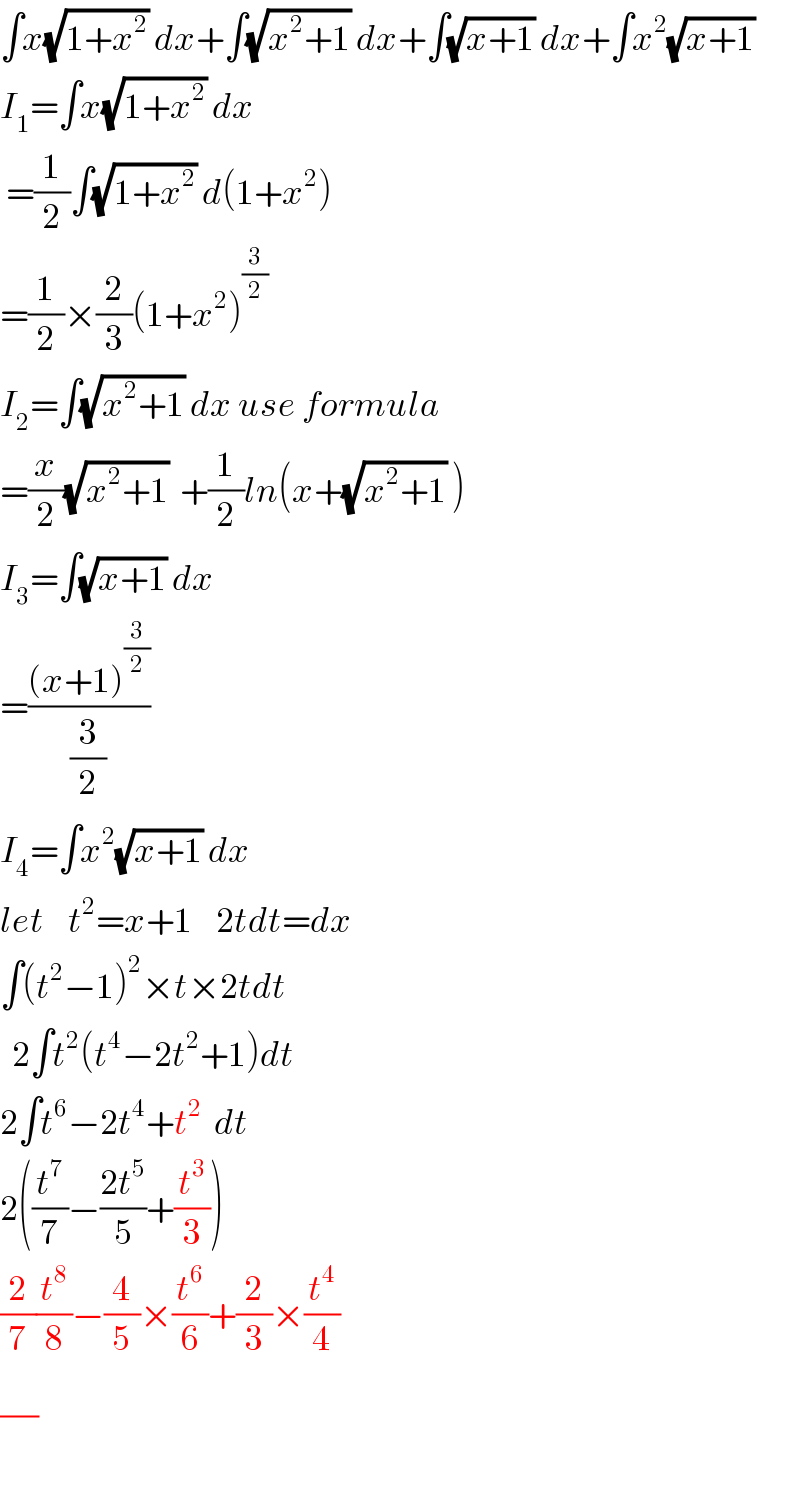
	Answered by MJS last updated on 25/Jul/18

	$\int x^{2} \sqrt{x + 1} d x = \frac{2}{7} (x^{2} - \frac{4 x}{5} + \frac{8}{15}) {(x + 1)}^{\frac{3}{2}}$ $[\begin{matrix} t = x + 1 \to d x = d t \\ \int {(t - 1)}^{2} \sqrt{t} d t = \int (t^{2} - 2 t + 1) \sqrt{t} d t = \int (t^{\frac{5}{2}} - 2 t^{\frac{3}{2}} + t^{\frac{1}{2}}) d t \\ \int t^{q} d t = \frac{1}{q + 1} t^{q + 1} \end{matrix}]$ $\int x \sqrt{x^{2} + 1} d x = \frac{1}{3} {(x^{2} + 1)}^{\frac{3}{2}}$ $[\begin{matrix} t = x^{2} + 1 \to d x = \frac{d t}{2 x} \\ \frac{1}{2} \int \sqrt{t} d t \\ \int t^{q} d t = \frac{1}{q + 1} t^{q + 1} \end{matrix}]$ $\int \sqrt{x^{2} + 1} d x = \frac{1}{2} (x \sqrt{x^{2} + 1} + \ln ∣ x + \sqrt{x^{2} + 1} ∣)$ $[\begin{matrix} t = \arctan x \to d x = \sec^{2} t d t \\ \int \sec^{2} t \sqrt{1 + \tan^{2} t} d t = \int \sec^{3} t d t \\ \int \sec^{n} t d t = \frac{\sec^{n - 2} t \tan t}{n - 1} + \frac{n - 2}{n - 1} \int \sec^{n - 2} t d t \end{matrix}]$ $\int \sqrt{x + 1} d x = \frac{2}{3} {(x + 1)}^{\frac{3}{2}}$ $[\int {(x + a)}^{q} d x = \frac{1}{q + 1} {(x + a)}^{q + 1}]$
	Answered by maxmathsup by imad last updated on 25/Jul/18
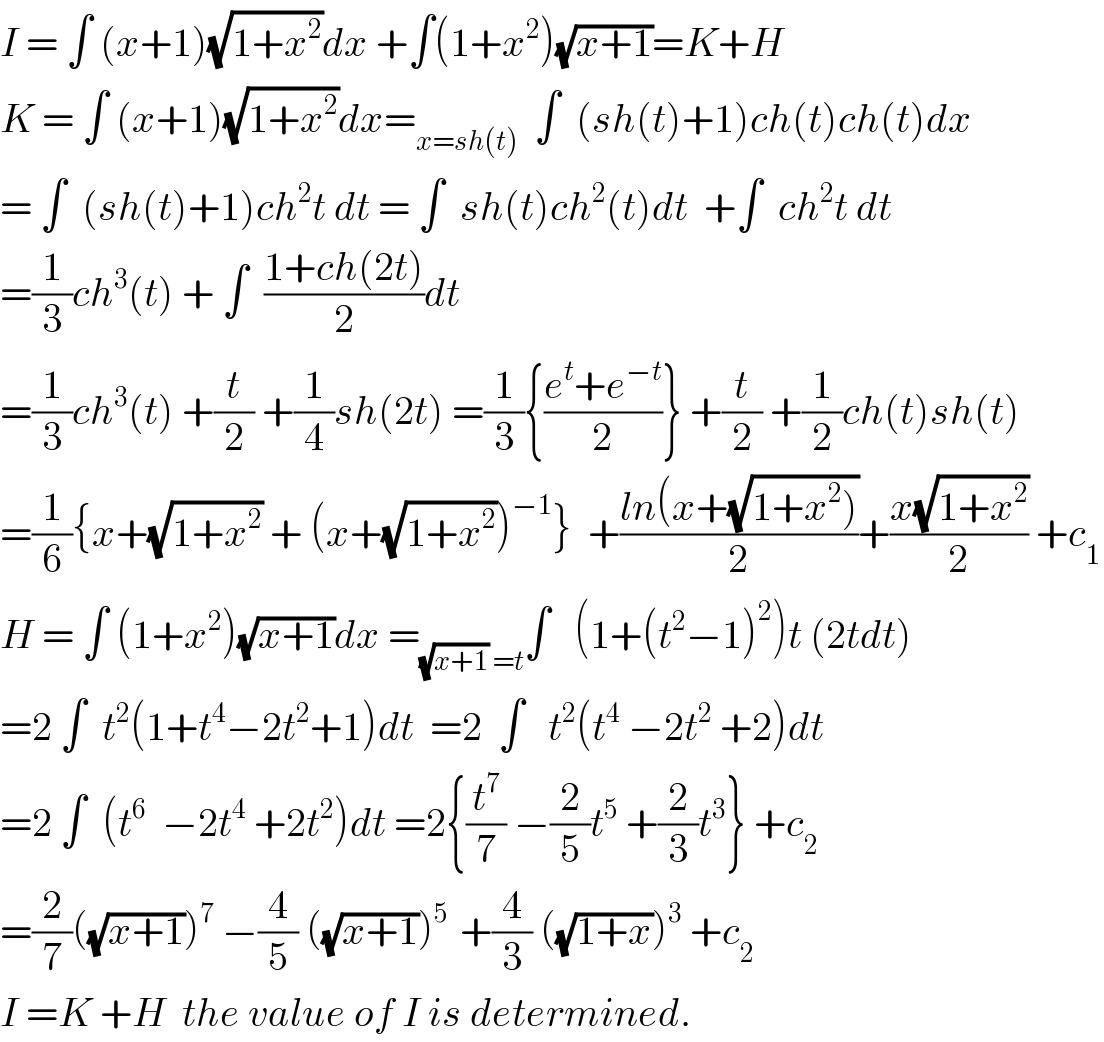
	$I = ∫ (x+1)(√(1+x^2 ))dx +∫(1+x^2 )(√(x+1))=K+H K = ∫ (x+1)(√(1+x^2 ))dx=_(x=sh(t)) ∫ (sh(t)+1)ch(t)ch(t)dx = ∫ (sh(t)+1)ch^2 t dt = ∫ sh(t)ch^2 (t)dt +∫ ch^2 t dt =(1/3)ch^3 (t) + ∫ ((1+ch(2t))/2)dt =(1/3)ch^3 (t) +(t/2) +(1/4)sh(2t) =(1/3){((e^t +e^(−t) )/2)} +(t/2) +(1/2)ch(t)sh(t) =(1/6){x+(√(1+x^2 )) + (x+(√(1+x^2 )))^(−1) } +((ln(x+(√(1+x^2 ))))/2)+((x(√(1+x^2 )))/2) +c_1 H = ∫ (1+x^2 )(√(x+1))dx =_((√(x+1)) =t) ∫ (1+(t^2 −1)^2 )t (2tdt) =2 ∫ t^2 (1+t^4 −2t^2 +1)dt =2 ∫ t^2 (t^4 −2t^2 +2)dt =2 ∫ (t^6 −2t^4 +2t^2 )dt =2{(t^7 /7) −(2/5)t^5 +(2/3)t^3 } +c_2 =(2/7)((√(x+1)))^7 −(4/5) ((√(x+1)))^(5 ) +(4/3) ((√(1+x)))^3 +c_2 I =K +H the value of I is determined.$
	$I = \int (x + 1) \sqrt{1 + x^{2}} d x + \int (1 + x^{2}) \sqrt{x + 1} = K + H$ $K = \int (x + 1) \sqrt{1 + x^{2}} d x =_{x = s h (t)} \int (s h (t) + 1) c h (t) c h (t) d x$ $= \int (s h (t) + 1) {c h}^{2} t d t = \int s h (t) {c h}^{2} (t) d t + \int {c h}^{2} t d t$ $= \frac{1}{3} {c h}^{3} (t) + \int \frac{1 + c h (2 t)}{2} d t$ $= \frac{1}{3} {c h}^{3} (t) + \frac{t}{2} + \frac{1}{4} s h (2 t) = \frac{1}{3} {\frac{e^{t} + e^{- t}}{2}} + \frac{t}{2} + \frac{1}{2} c h (t) s h (t)$ $= \frac{1}{6} {x + \sqrt{1 + x^{2}} + {(x + \sqrt{1 + x^{2}})}^{- 1}} + \frac{l n (x + \sqrt{1 + x^{2})}}{2} + \frac{x \sqrt{1 + x^{2}}}{2} + c_{1}$ $H = \int (1 + x^{2}) \sqrt{x + 1} d x =_{\sqrt{x + 1} = t} \int (1 + {(t^{2} - 1)}^{2}) t (2 t d t)$ $= 2 \int t^{2} (1 + t^{4} - 2 t^{2} + 1) d t = 2 \int t^{2} (t^{4} - 2 t^{2} + 2) d t$ $= 2 \int (t^{6} - 2 t^{4} + 2 t^{2}) d t = 2 {\frac{t^{7}}{7} - \frac{2}{5} t^{5} + \frac{2}{3} t^{3}} + c_{2}$ $= \frac{2}{7} {(\sqrt{x + 1})}^{7} - \frac{4}{5} {(\sqrt{x + 1})}^{5} + \frac{4}{3} {(\sqrt{1 + x})}^{3} + c_{2}$ $I = K + H t h e v a l u e o f I i s d e t e r m i n e d .$
	Commented by maxmathsup by imad last updated on 25/Jul/18
	$error at line 5 K =(1/3)ch^3 (t) +(t/2)sh(2t)=(1/3){((e^t +e^(−t) )/2)}^3 +(t/2) +(1/2)ch(t)sh(t) =(1/(24)){ x+(√(1+x^2 ))+(x+(√(1+x^2 )))^(−1) }^3 +((ln(x+(√(1+x^2 ))))/2) +((x(√(1+x^2 )))/2) +c_1$
	$e r r o r a t l i n e 5$ $K = \frac{1}{3} {c h}^{3} (t) + \frac{t}{2} s h (2 t) = \frac{1}{3} {\frac{e^{t} + e^{- t}}{2}}^{3} + \frac{t}{2} + \frac{1}{2} c h (t) s h (t)$ $= \frac{1}{24} {x + \sqrt{1 + x^{2}} + {(x + \sqrt{1 + x^{2}})}^{- 1}}^{3} + \frac{l n (x + \sqrt{1 + x^{2})}}{2} + \frac{x \sqrt{1 + x^{2}}}{2} + c_{1}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum