find ∫ (x^2 −1)(√(x^2 +1))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 85166 by mathmax by abdo last updated on 19/Mar/20

$f i n d \int (x^{2} - 1) \sqrt{x^{2} + 1} d x$
Commented by john santu last updated on 21/Mar/20
$let K = ∫ x^2 (√(x^2 +1)) dx K = (1/2)∫ x { 2x(√(x^2 +1)) } dx K= (1/2) ∫ x { (√(x^2 +1)) d(x^2 +1) } = (1/2){ (2/3) x (x^2 +1)^(3/2) −∫ (x^2 +1)^(3/2) dx} = (1/3)x(x^2 +1)^(3/2) −(1/2) ∫ sec^5 u du [ x = tan u ] H= ∫ sec^5 u du = ∫ sec^3 u d(tan u) H = sec^3 u tan u −∫ tan u (3sec^3 u tan u )du H= sec^3 u tan u −3∫(sec^5 u−sec^3 u)du 4H = sec^3 u tan u +3∫ sec^3 u du H = (1/4)x (x^2 +1)^(3/2) +(3/4)sec^3 u du let J = ∫ (√(x^2 +1)) dx , [ x=tan t ] J = ∫ sec^3 t dt = ∫ sec t d(tan t) J = sec t tan t − ∫ tan^2 t sec t dt J = sec t tan t − ∫ (sec^3 t−sec t) dt 2J = sec t tan t +ln ∣ x+(√(x^2 +1)) ∣ J= (1/2)sec t tan t + (1/2)ln ∣x+(√(x^2 +1)) ∣ ∴ H = (1/4)x(x^2 +1)^(3/2) +(7/8)x(x^2 +1)^(3/2) + (7/8)ln ∣x+(√(x^2 +1)) ∣ +c K= (1/3)x(x^2 +1)^(3/2) −(1/5)H ∴ K =(1/3)x(x^2 +1)^(3/2) −(9/(40))x(x^2 +1)^(3/2) − (7/(40)) ln ∣x+(√(x^2 +1)) ∣ +c K = ((13)/(120))x(x^2 +1)^(3/2) −(7/(40))ln ∣x+(√(x^2 +1)) ∣ + c$
$let K = \int x^{2} \sqrt{x^{2} + 1} dx$ $K = \frac{1}{2} \int x {2 x \sqrt{x^{2} + 1}} dx$ $K = \frac{1}{2} \int x {\sqrt{x^{2} + 1} d (x^{2} + 1)}$ $= \frac{1}{2} {\frac{2}{3} x {(x^{2} + 1)}^{\frac{3}{2}} - \int {(x^{2} + 1)}^{\frac{3}{2}} dx}$ $= \frac{1}{3} x {(x^{2} + 1)}^{\frac{3}{2}} - \frac{1}{2} \int \sec^{5} u du$ $[x = \tan u]$ $H = \int \sec^{5} u du = \int \sec^{3} u d (\tan u)$ $H = \sec^{3} u \tan u - \int \tan u (3 \sec^{3} u \tan u) du$ $H = \sec^{3} u \tan u - 3 \int (\sec^{5} u - \sec^{3} u) du$ $4 H = \sec^{3} u \tan u + 3 \int \sec^{3} u du$ $H = \frac{1}{4} x {(x^{2} + 1)}^{\frac{3}{2}} + \frac{3}{4} \sec^{3} u du$ $let J = \int \sqrt{x^{2} + 1} dx, [x = \tan t]$ $J = \int \sec^{3} t dt = \int \sec t d (\tan t)$ $J = \sec t \tan t - \int \tan^{2} t \sec t dt$ $J = \sec t \tan t - \int (\sec^{3} t - \sec t) dt$ $2 J = \sec t \tan t + \ln ∣ x + \sqrt{x^{2} + 1} ∣$ $J = \frac{1}{2} \sec t \tan t + \frac{1}{2} \ln ∣ x + \sqrt{x^{2} + 1} ∣$ $∴ H = \frac{1}{4} x {(x^{2} + 1)}^{\frac{3}{2}} + \frac{7}{8} x {(x^{2} + 1)}^{\frac{3}{2}} +$ $\frac{7}{8} \ln ∣ x + \sqrt{x^{2} + 1} ∣ + c$ $K = \frac{1}{3} x {(x^{2} + 1)}^{\frac{3}{2}} - \frac{1}{5} H$ $∴ K = \frac{1}{3} x {(x^{2} + 1)}^{\frac{3}{2}} - \frac{9}{40} x {(x^{2} + 1)}^{\frac{3}{2}} -$ $\frac{7}{40} \ln ∣ x + \sqrt{x^{2} + 1} ∣ + c$ $K = \frac{13}{120} x {(x^{2} + 1)}^{\frac{3}{2}} - \frac{7}{40} \ln ∣ x + \sqrt{x^{2} + 1} ∣ + c$
Commented by mathmax by abdo last updated on 21/Mar/20

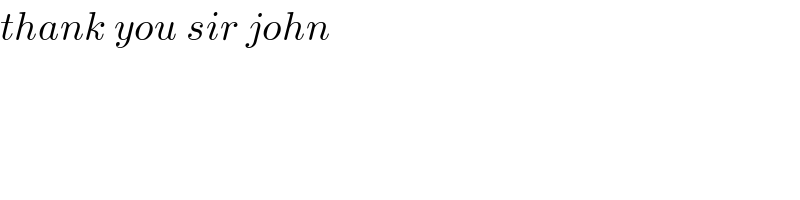
$t h a n k y o u s i r j o h n$
Commented by mathmax by abdo last updated on 21/Mar/20

$A = \int (x^{2} - 1) \sqrt{x^{2} + 1} d x f o r t h i s k i n d o f i n t e g r a l s w e d o t h e$ $c h a n g e m e n t x = s h (t) \Rightarrow A = \int ({s h}^{2} t - 1) c h (t) c h (t) d t$ $A = \int ({s h}^{2} t - 1) {c h}^{2} t d t = \int (\frac{c h (2 t) - 1}{2} - 1) (\frac{c h (2 t) + 1}{2}) d t$ $= \frac{1}{4} \int (c h (2 t) - 3) (c h (2 t) + 1) d t$ $= \frac{1}{4} \int ({c h}^{2} (2 t) + c h (2 t) - 3 c h (2 t) - 3) d t$ $= \frac{1}{4} \int ({c h}^{2} (2 t) - 2 c h (2 t) - 3) d t$ $= \frac{1}{8} \int (1 + c h (4 t)) d t - \frac{1}{2} \int c h (2 t) - \frac{3}{4} t + C$ $= \frac{1}{8} t + \frac{1}{32} s h (4 t) - \frac{1}{4} s h (2 t) - \frac{3}{4} t + C$ $= - \frac{5}{8} t + \frac{1}{16} s h (2 t) c h (2 t) - \frac{1}{2} s h (2 t) c h (2 t) + C$ $= - \frac{5}{8} t + \frac{1}{8} s h (t) c h (t) (1 + 2 {s h}^{2} t) - s h (t) {c h}^{2} t + C$ $= - \frac{5}{8} l n (x + \sqrt{1 + x^{2}}) + \frac{1}{8} x \sqrt{1 + x^{2}} (1 + 2 x^{2}) - x (1 + x^{2}) + C$
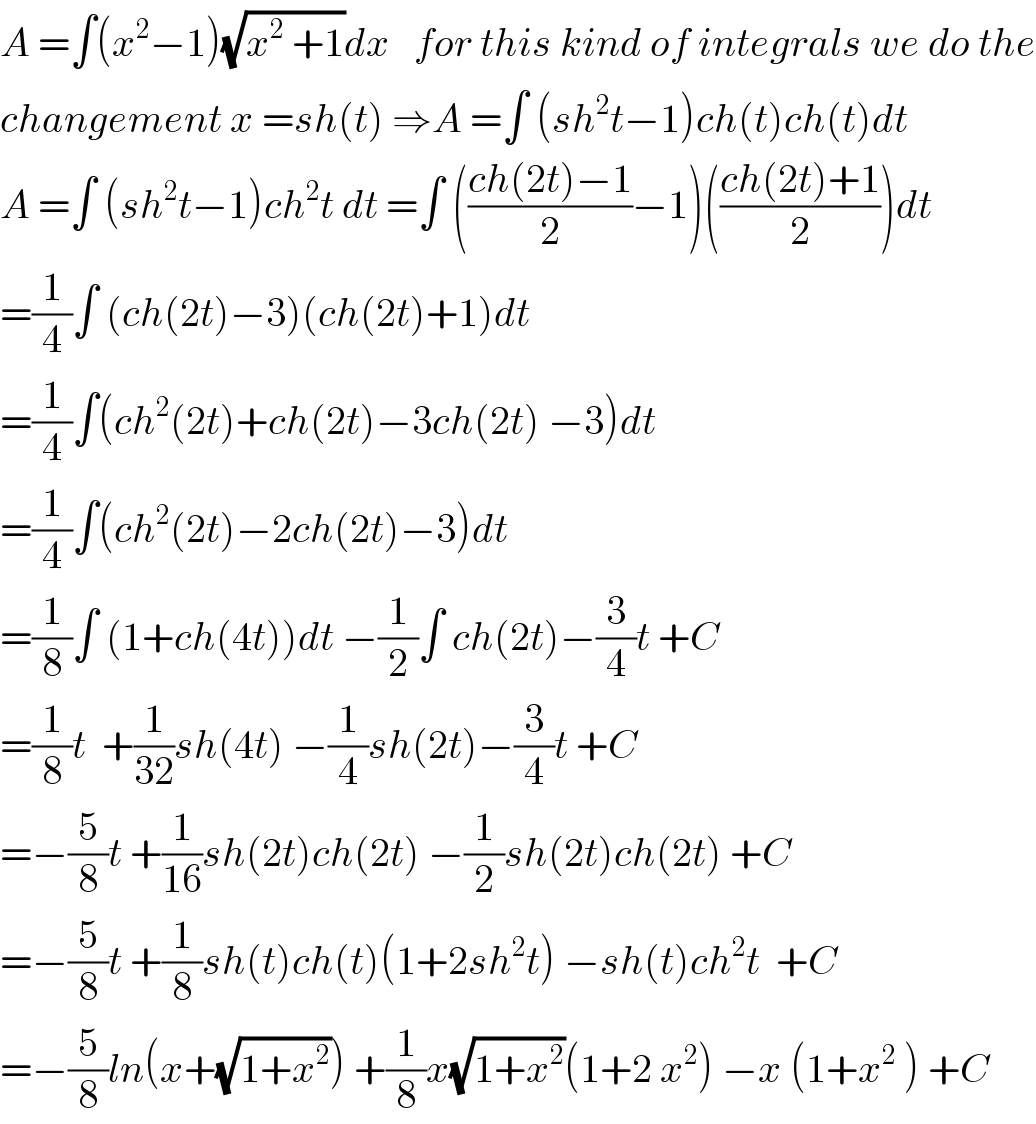
	Answered by MJS last updated on 20/Mar/20

	$\int (x^{2} - 1) \sqrt{x^{2} + 1} d x =$ $[t = x + \sqrt{x^{2} + 1} \to d x = \frac{\sqrt{x^{2} + 1}}{x + \sqrt{x^{2} + 1}} d t]$ $= \int (\frac{t^{3}}{16} - \frac{t}{4} - \frac{5}{8 t} - \frac{1}{4 t^{3}} + \frac{1}{16 t^{5}}) d t =$ $= \frac{t^{4}}{64} - \frac{t^{2}}{8} - \frac{5}{8} \ln t + \frac{1}{8 t^{2}} - \frac{1}{64 t^{4}} =$ $= \frac{t^{8} - 8 t^{6} + 8 t^{2} - 1}{64 t^{4}} - \frac{5}{8} \ln t =$ $= \frac{x (2 x^{2} - 3) \sqrt{x^{2} + 1}}{8} - \frac{5}{8} \ln (x + \sqrt{x^{2} + 1}) + C$
	Commented by mathmax by abdo last updated on 20/Mar/20

	$t h a n k y o u s i r m j s$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum