
Question and Answers Forum
Question Number 74890 by abdomathmax last updated on 03/Dec/19

Commented by mathmax by abdo last updated on 04/Dec/19
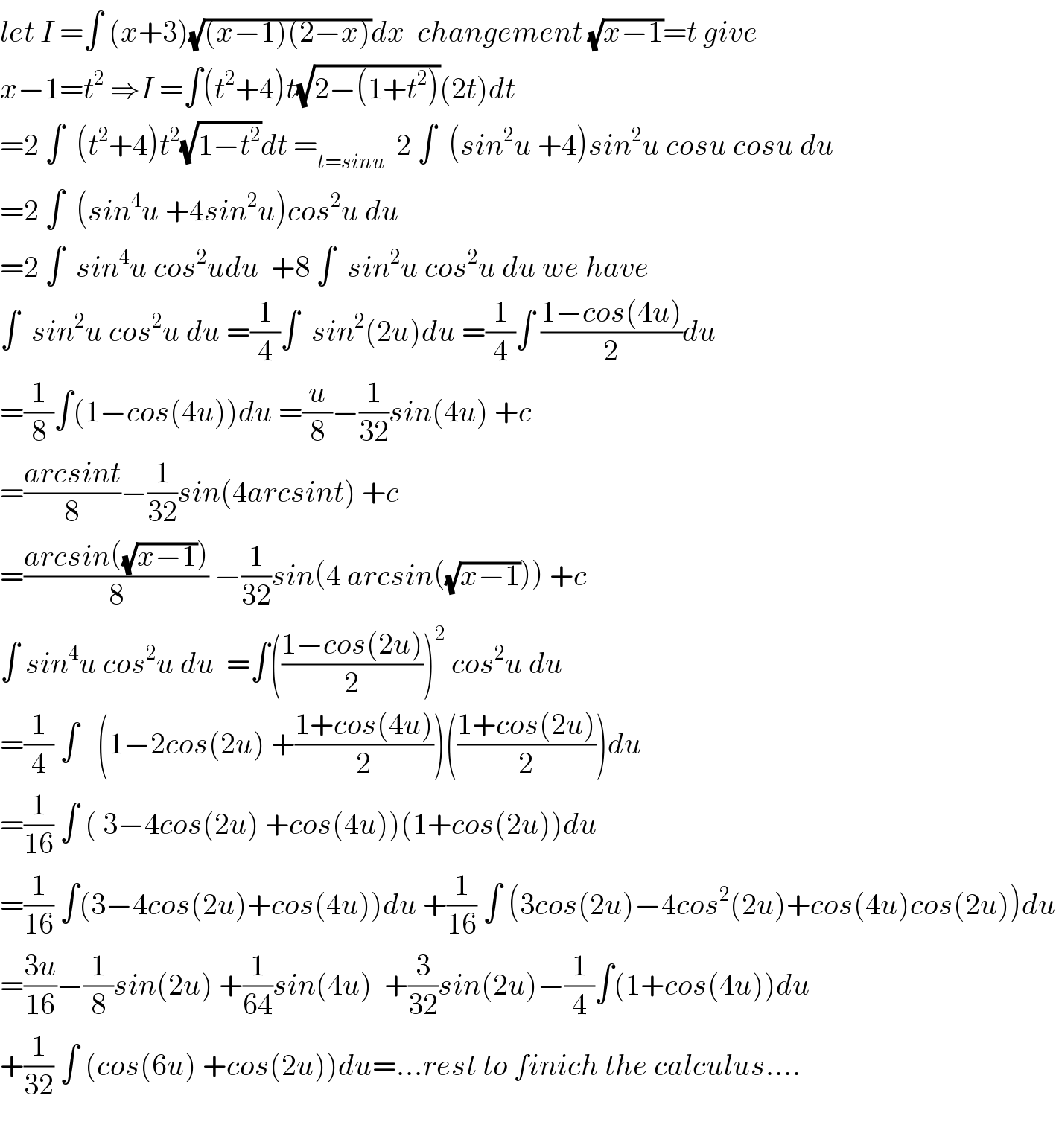
Answered by MJS last updated on 03/Dec/19
![∫(x+3)(√((x−1)(2−x)))dx= =∫(x+3)(√((1/4)−(x−(3/2))^2 ))dx= [t=2x−3 → dx=(dt/2)] =(1/8)∫(t+9)(√(1−t^2 ))dt= =(1/8)∫t(√(1−t^2 ))dt+(9/8)∫(√(1−t^2 ))dt= [u=arcsin t → dt=(√(1−t^2 ))du] =(1/8)∫sin u cos^2 u du+(9/8)∫cos^2 u du= =−(1/(24))cos^3 u+(9/(16))(u+sin u cos u)= =−(1/(24))(1−t^2 )^(3/2) +(9/(16))t(√(1−t^2 ))+(9/(16))arcsin t = =((1/(24))t^2 +(9/(16))t−(1/(24)))(√(1−t^2 ))+(9/(16))arcsin t = =((1/3)x^2 +(5/4)x−((65)/(24)))(√((x−1)(2−x)))+(9/(16))arcsin (2x−3) +C](Q74902.png)
Commented by mathmax by abdo last updated on 03/Dec/19
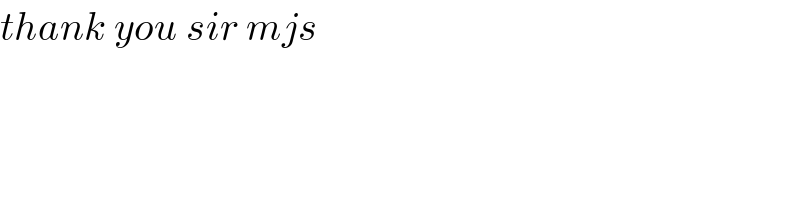
| ||
Question and Answers Forum | ||
Question Number 74890 by abdomathmax last updated on 03/Dec/19 | ||
 | ||
Commented by mathmax by abdo last updated on 04/Dec/19 | ||
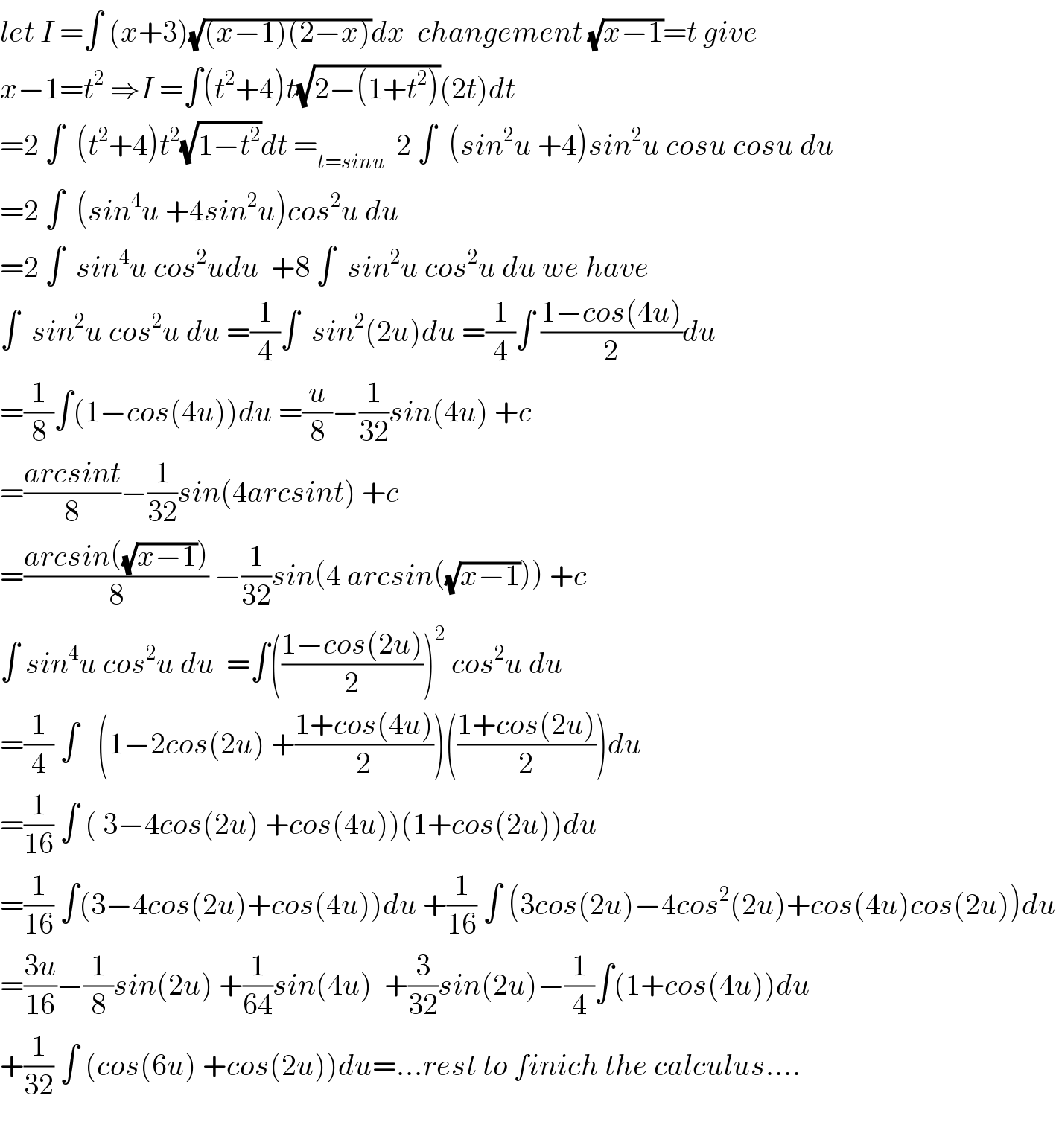 | ||
Answered by MJS last updated on 03/Dec/19 | ||
![∫(x+3)(√((x−1)(2−x)))dx= =∫(x+3)(√((1/4)−(x−(3/2))^2 ))dx= [t=2x−3 → dx=(dt/2)] =(1/8)∫(t+9)(√(1−t^2 ))dt= =(1/8)∫t(√(1−t^2 ))dt+(9/8)∫(√(1−t^2 ))dt= [u=arcsin t → dt=(√(1−t^2 ))du] =(1/8)∫sin u cos^2 u du+(9/8)∫cos^2 u du= =−(1/(24))cos^3 u+(9/(16))(u+sin u cos u)= =−(1/(24))(1−t^2 )^(3/2) +(9/(16))t(√(1−t^2 ))+(9/(16))arcsin t = =((1/(24))t^2 +(9/(16))t−(1/(24)))(√(1−t^2 ))+(9/(16))arcsin t = =((1/3)x^2 +(5/4)x−((65)/(24)))(√((x−1)(2−x)))+(9/(16))arcsin (2x−3) +C](Q74902.png) | ||
| ||
Commented by mathmax by abdo last updated on 03/Dec/19 | ||
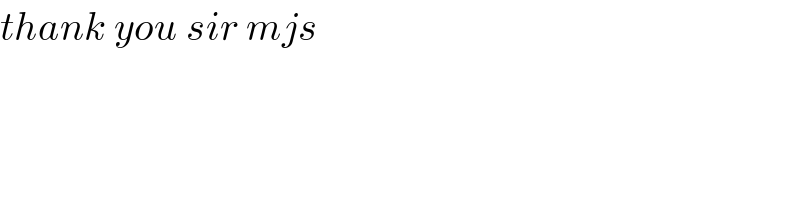 | ||