
Question and Answers Forum
Question Number 62855 by mathmax by abdo last updated on 26/Jun/19
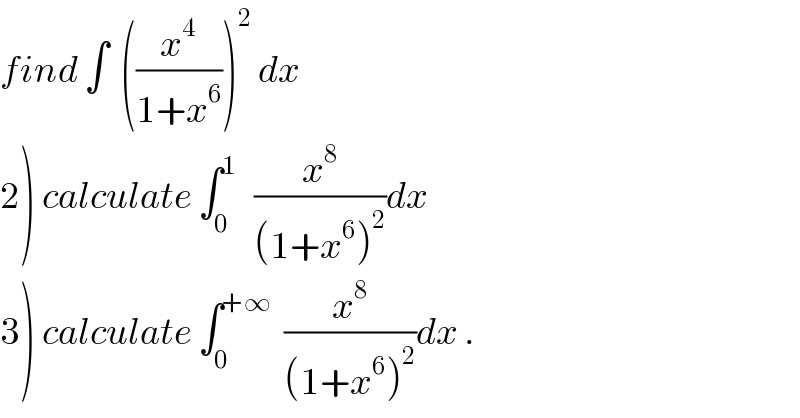
Commented by mathmax by abdo last updated on 27/Jun/19
![1) let I =∫ (x^8 /((1+x^6 )^2 ))dx ⇒I =∫ (x^8 /((1+(x^3 )^2 )^2 ))dx changement x^3 =tanθ give x =(tanθ)^(1/(3 )) ⇒ I =∫ (((tanθ)^(8/3) )/((1+tan^2 θ)^2 )) (1/3)(1+tan^2 θ)(tanθ)^(−(2/3)) dθ =(1/3) ∫ ((tan^2 θ)/(1+tan^2 θ)) dθ =(1/3) ∫ ((sin^2 θ)/(cos^2 θ)) cos^2 θ dθ =(1/3) ∫ sin^2 θ dθ =(1/3) ∫((1−cos(2θ))/2)dθ =(θ/6) −(1/(12)) sin(2θ) +c but θ =arctan(x^3 ) sin(2θ) =2sinθ cosθ =2 sin(arctan(x^3 ))cos(arctan(x^3 )) =2 (x^3 /(√(1+x^6 ))) .(1/(√(1+x^6 ))) =((2x^3 )/(1+x^6 )) ⇒ I =(1/6) arctan(x^3 )−(1/6)(x^3 /(1+x^6 )) +c 2) ∫_0 ^1 (x^8 /((1+x^6 )^2 ))dx =(1/6)[arctan(x^3 )−(x^3 /(1+x^6 ))]_0 ^1 =(1/6){(π/4) −(1/2)} 3) ∫_0 ^∞ (x^8 /((1+x^6 )^2 ))dx =(1/6)[ arctan(x^3 )−(x^3 /(1+x^6 ))]_0 ^(+∞) =(1/6) (π/2) =(π/(12)) . ×](Q63002.png)
| ||
Question and Answers Forum | ||
Question Number 62855 by mathmax by abdo last updated on 26/Jun/19 | ||
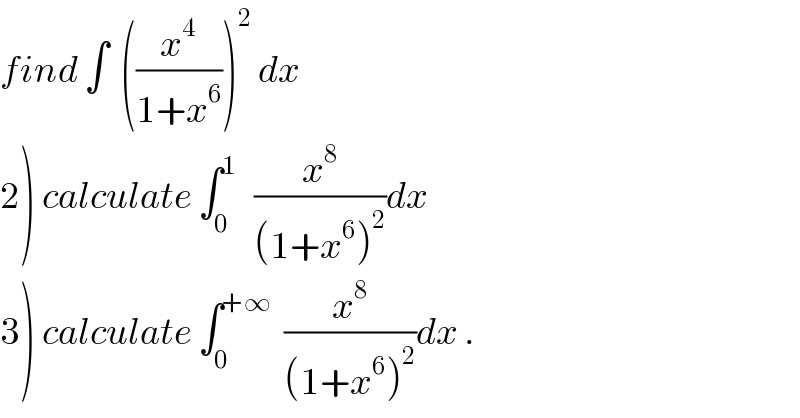 | ||
Commented by mathmax by abdo last updated on 27/Jun/19 | ||
![1) let I =∫ (x^8 /((1+x^6 )^2 ))dx ⇒I =∫ (x^8 /((1+(x^3 )^2 )^2 ))dx changement x^3 =tanθ give x =(tanθ)^(1/(3 )) ⇒ I =∫ (((tanθ)^(8/3) )/((1+tan^2 θ)^2 )) (1/3)(1+tan^2 θ)(tanθ)^(−(2/3)) dθ =(1/3) ∫ ((tan^2 θ)/(1+tan^2 θ)) dθ =(1/3) ∫ ((sin^2 θ)/(cos^2 θ)) cos^2 θ dθ =(1/3) ∫ sin^2 θ dθ =(1/3) ∫((1−cos(2θ))/2)dθ =(θ/6) −(1/(12)) sin(2θ) +c but θ =arctan(x^3 ) sin(2θ) =2sinθ cosθ =2 sin(arctan(x^3 ))cos(arctan(x^3 )) =2 (x^3 /(√(1+x^6 ))) .(1/(√(1+x^6 ))) =((2x^3 )/(1+x^6 )) ⇒ I =(1/6) arctan(x^3 )−(1/6)(x^3 /(1+x^6 )) +c 2) ∫_0 ^1 (x^8 /((1+x^6 )^2 ))dx =(1/6)[arctan(x^3 )−(x^3 /(1+x^6 ))]_0 ^1 =(1/6){(π/4) −(1/2)} 3) ∫_0 ^∞ (x^8 /((1+x^6 )^2 ))dx =(1/6)[ arctan(x^3 )−(x^3 /(1+x^6 ))]_0 ^(+∞) =(1/6) (π/2) =(π/(12)) . ×](Q63002.png) | ||