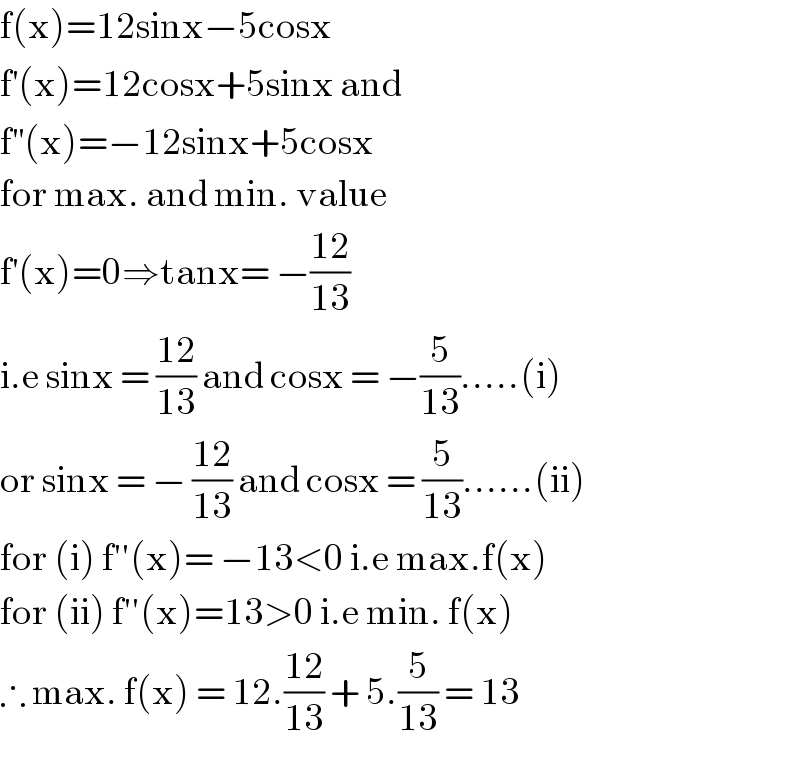Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 66115 by Rio Michael last updated on 09/Aug/19

$$find\mid z\mid wherez=\frac{{(1+i\sqrt{3})}^3}{{(1-i)}^3}$$$$findthemaximumvalueof12sinx-5cosx$$

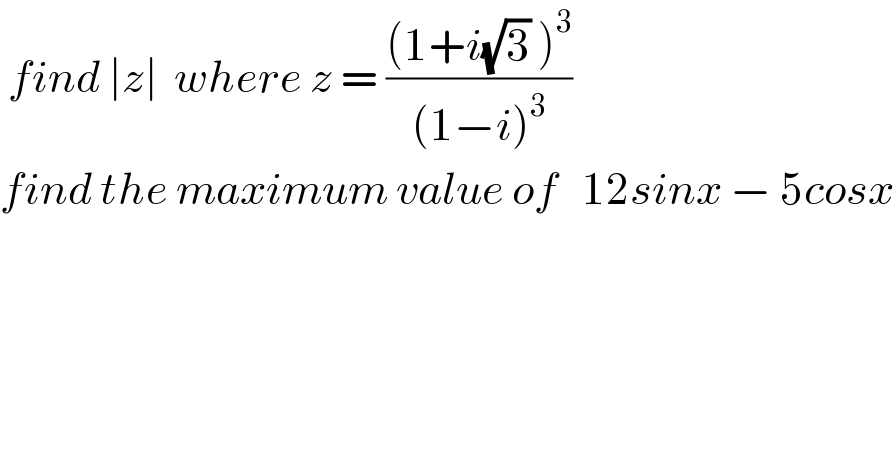
Commented by mathmax by abdo last updated on 09/Aug/19

$$\mid z\mid =\frac{\mid 1+i\sqrt{3}{\mid }^3}{\mid 1-i{\mid }^3}and\mid 1+i\sqrt{3}\mid =\sqrt{1+3}=2$$$$\mid 1-i\mid =\sqrt{2}\Rightarrow \mid z\mid =\frac{2^3}{{\left(\sqrt{2}\right)}^3}=\frac{2^3}{2\sqrt{2}}=\frac{4}{\sqrt{2}}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$$

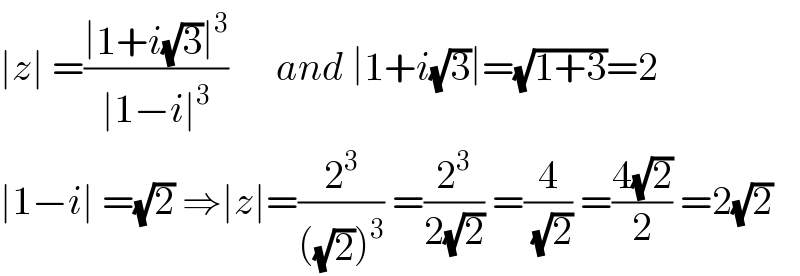
Commented by mathmax by abdo last updated on 09/Aug/19

$$letf\left(x\right)=12sinx-5cosxfis2\pi periodicf\left(x\right)=0\iff x=arctan\left(\frac{5}{12}\right)$$$$f^{{}^{\prime }}\left(x\right)=12cosx+5sinx$$$$f^{{}^{\prime }}\left(x\right)=0\iff 12cosx+5sinx=0\Rightarrow 5sinx=-12cosx\Rightarrow$$$$tanx=-\frac{12}{5}\Rightarrow x=-arctan\left(\frac{12}{5}\right)varationon[-\pi ,\pi ]$$$$x-\pi -arctan\left(\frac{12}{5}\right)0arctan\left(\frac{5}{12}\right)\pi$$$$f\left(x\right)5decr{\alpha }_0?-5incr0inc5$$$$f(-arctan\left(\frac{12}{5}\right))=-12sin\left(arctan\left(\frac{12}{5}\right)\right)-5cos\left(arctan\left(\frac{12}{5}\right)\right)$$$$=-12\frac{\frac{12}{5}}{\sqrt{1+{\left(\frac{12}{5}\right)}^2}}-5\times \frac{1}{\sqrt{1+{\left(\frac{12}{5}\right)}^2}}={\alpha }_0$$$$f\left(arctan\left(\frac{5}{12}\right)\right)=12sin\left(arctan\left(\frac{5}{12}\right)\right)-5cos\left(arctan\left(\frac{5}{12}\right)\right)$$$$=12\times \frac{\frac{5}{12}}{\sqrt{1+{\left(\frac{5}{12}\right)}^2}}-5\times \frac{1}{\sqrt{1+{\left(\frac{5}{12}\right)}^2}}=0$$$$\Rightarrow max{}_{x\in R}f\left(x\right)=5$$

Commented by Rio Michael last updated on 09/Aug/19

$$thankyousir$$

Commented by Prithwish sen last updated on 09/Aug/19

$$\mathrm{f}\left(\mathrm{x}\right)=12\mathrm{sinx}-5\mathrm{cosx}$$$${\mathrm{f}}^{{}^{\prime }}\left(\mathrm{x}\right)=12\mathrm{cosx}+5\mathrm{sinx}\mathrm{and}$$$${\mathrm{f}}^{{}^{″}}\left(\mathrm{x}\right)=-12\mathrm{sinx}+5\mathrm{cosx}$$$$\mathrm{for}\max .\mathrm{and}\min .\mathrm{value}$$$${\mathrm{f}}^{{}^{\prime }}\left(\mathrm{x}\right)=0\Rightarrow \mathrm{tanx}=-\frac{12}{13}$$$$\mathrm{i}.\mathrm{e}\mathrm{sinx}=\frac{12}{13}\mathrm{and}\mathrm{cosx}=-\frac{5}{13}.....\left(\mathrm{i}\right)$$$$\mathrm{or}\mathrm{sinx}=-\frac{12}{13}\mathrm{and}\mathrm{cosx}=\frac{5}{13}......\left(\mathrm{ii}\right)$$$$\mathrm{for}\left(\mathrm{i}\right){\mathrm{f}}^{″}\left(\mathrm{x}\right)=-13<0\mathrm{i}.\mathrm{e}\max .\mathrm{f}\left(\mathrm{x}\right)$$$$\mathrm{for}\left(\mathrm{ii}\right){\mathrm{f}}^{″}\left(\mathrm{x}\right)=13>0\mathrm{i}.\mathrm{e}\min .\mathrm{f}\left(\mathrm{x}\right)$$$$\therefore \max .\mathrm{f}\left(\mathrm{x}\right)=12.\frac{12}{13}+5.\frac{5}{13}=13$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com