
Question and Answers Forum
Question Number 55280 by Abdo msup. last updated on 20/Feb/19
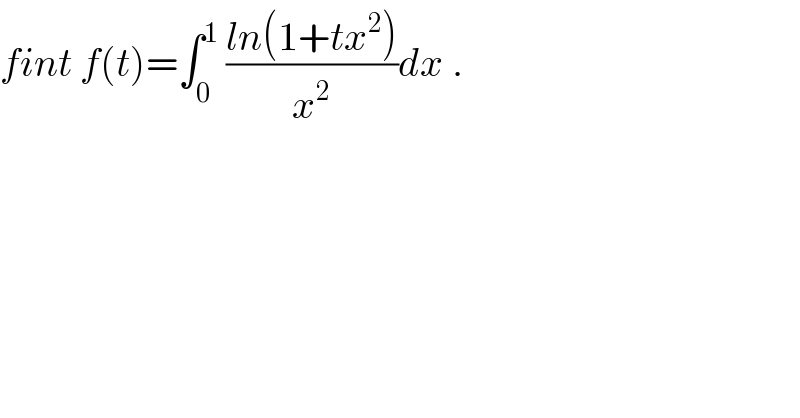
Commented by maxmathsup by imad last updated on 20/Feb/19
![we have f^′ (t) =∫_0 ^1 (∂/∂t)(((ln(1+tx^2 ))/x^2 ))dx =∫_0 ^1 (1/x^2 ) (x^2 /(1+tx^2 ))dx = ∫_0 ^1 (dx/(1+tx^2 )) so if t≥0 we get f^′ (t)=_((√t)x =u) ∫_0 ^(√t) (du/((√t)(1+u^2 ))) =(1/(√t))[arctan(u)]_0 ^(√t) =((arctan((√t)))/(√t)) ⇒f(t) =∫_0 ^t ((arctan((√u)))/(√u)) du +λ λ=f(0)=0 ⇒f(t) =∫_0 ^t ((arctan((√u)))/(√u)) du =_((√u)=x) ∫_0 ^(√t) ((arctanx)/x) (2x)dx =2 ∫_0 ^(√t) arctanx dx by parts f(t)=2{ [xarctanx]_0 ^(√t) −∫_0 ^(√t) (x/(1+x^2 ))dx} =2{(√t)arctan((√t)) −[(1/2)ln(1+x^2 )]_0 ^(√t) ⇒f(t)=2(√t)arctan((√t))−ln(1+t) . it t<0 we get f^′ (t) =∫_0 ^1 (dx/(1−(−t)x^2 )) =∫_0 ^1 (dx/((1−(√(−t))x)(1+(√(−t))x))) =(1/2)∫_0 ^1 ( (1/(1−(√(−t))x)) +(1/(1+(√(−t))x)))dx =(1/(2(√(−t)))) { ∫_0 ^1 ((√(−t))/(1−(√(−t))x)) +∫_0 ^1 ((√(−t))/(1+(√(−t))x))dx} =(1/(2(√(−t))))[ln∣1+(√(−t))x∣−ln∣1−(√(−t))x∣]_(x=0) ^(x=1) =(1/(2(√(−t)))) ln∣((1+(√(−t)))/(1−(√(−t))))∣ ⇒ f(t) =∫(1/(2(√(−t))))ln∣((1+(√(−t)))/(1−(√(−t))))∣dt +c =_((√(−t))=x) ∫ (1/(2x))ln∣((1+x)/(1−x))∣(−2x)dx +c = c−∫ ln∣1+x∣dx+∫ln∣1−x∣dx](Q55299.png)
Answered by tm888 last updated on 20/Feb/19

| ||
Question and Answers Forum | ||
Question Number 55280 by Abdo msup. last updated on 20/Feb/19 | ||
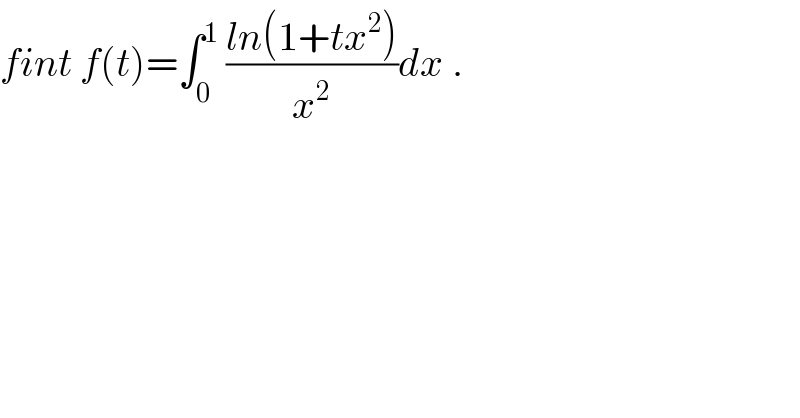 | ||
Commented by maxmathsup by imad last updated on 20/Feb/19 | ||
![we have f^′ (t) =∫_0 ^1 (∂/∂t)(((ln(1+tx^2 ))/x^2 ))dx =∫_0 ^1 (1/x^2 ) (x^2 /(1+tx^2 ))dx = ∫_0 ^1 (dx/(1+tx^2 )) so if t≥0 we get f^′ (t)=_((√t)x =u) ∫_0 ^(√t) (du/((√t)(1+u^2 ))) =(1/(√t))[arctan(u)]_0 ^(√t) =((arctan((√t)))/(√t)) ⇒f(t) =∫_0 ^t ((arctan((√u)))/(√u)) du +λ λ=f(0)=0 ⇒f(t) =∫_0 ^t ((arctan((√u)))/(√u)) du =_((√u)=x) ∫_0 ^(√t) ((arctanx)/x) (2x)dx =2 ∫_0 ^(√t) arctanx dx by parts f(t)=2{ [xarctanx]_0 ^(√t) −∫_0 ^(√t) (x/(1+x^2 ))dx} =2{(√t)arctan((√t)) −[(1/2)ln(1+x^2 )]_0 ^(√t) ⇒f(t)=2(√t)arctan((√t))−ln(1+t) . it t<0 we get f^′ (t) =∫_0 ^1 (dx/(1−(−t)x^2 )) =∫_0 ^1 (dx/((1−(√(−t))x)(1+(√(−t))x))) =(1/2)∫_0 ^1 ( (1/(1−(√(−t))x)) +(1/(1+(√(−t))x)))dx =(1/(2(√(−t)))) { ∫_0 ^1 ((√(−t))/(1−(√(−t))x)) +∫_0 ^1 ((√(−t))/(1+(√(−t))x))dx} =(1/(2(√(−t))))[ln∣1+(√(−t))x∣−ln∣1−(√(−t))x∣]_(x=0) ^(x=1) =(1/(2(√(−t)))) ln∣((1+(√(−t)))/(1−(√(−t))))∣ ⇒ f(t) =∫(1/(2(√(−t))))ln∣((1+(√(−t)))/(1−(√(−t))))∣dt +c =_((√(−t))=x) ∫ (1/(2x))ln∣((1+x)/(1−x))∣(−2x)dx +c = c−∫ ln∣1+x∣dx+∫ln∣1−x∣dx](Q55299.png) | ||
Answered by tm888 last updated on 20/Feb/19 | ||
 | ||