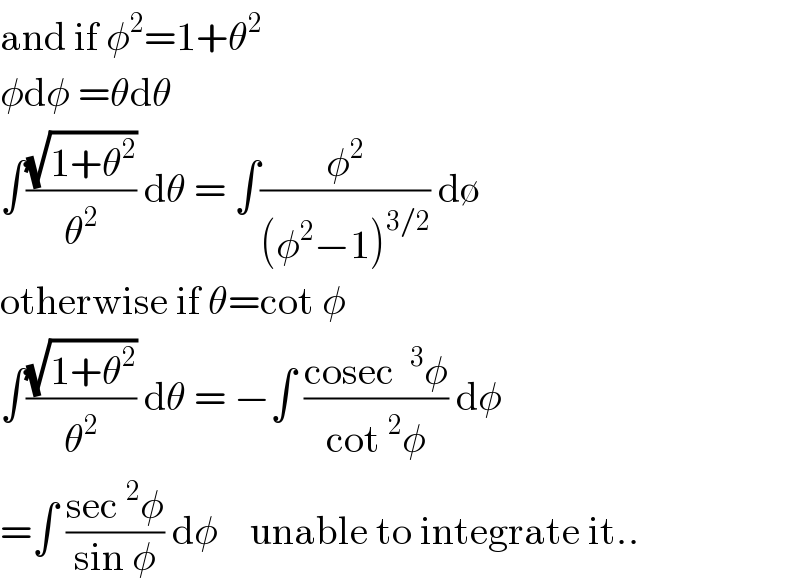Question and Answers Forum
Question Number 11433 by FilupS last updated on 26/Mar/17
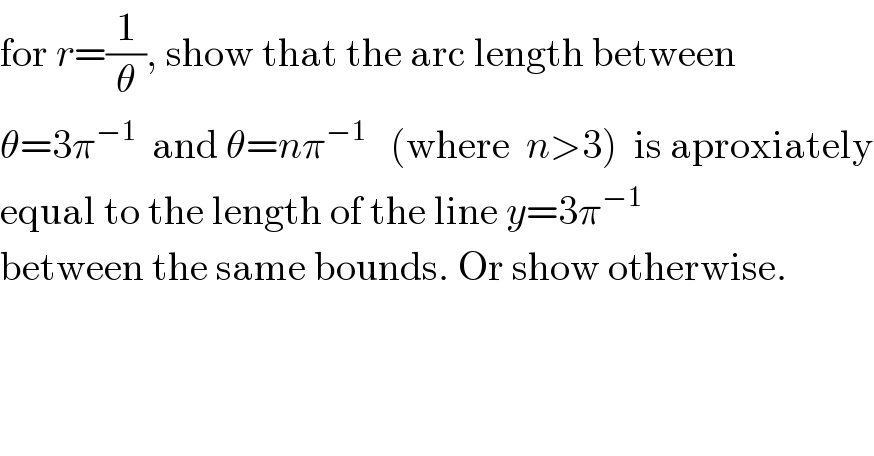
Commented by FilupS last updated on 26/Mar/17

Commented by @ANTARES_VY last updated on 26/Mar/17

Commented by FilupS last updated on 26/Mar/17

Commented by mrW1 last updated on 26/Mar/17
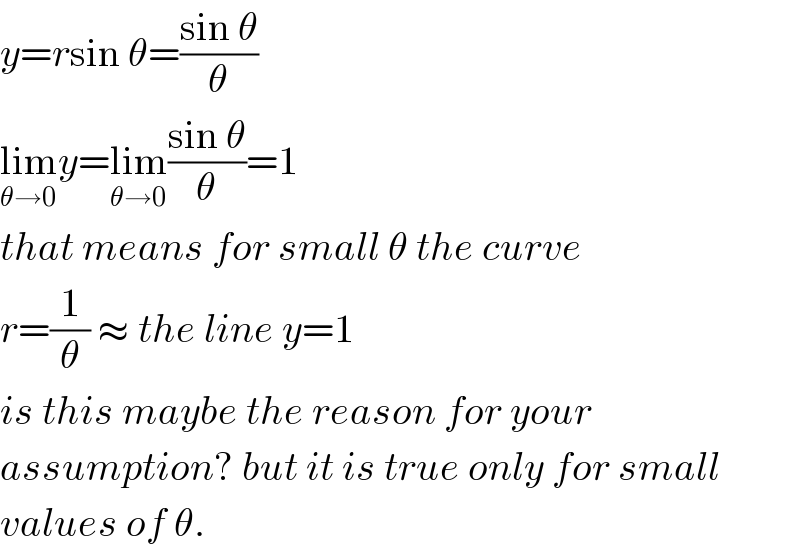
Commented by FilupS last updated on 26/Mar/17
Answered by mrW1 last updated on 26/Mar/17
![curve r=(1/θ): (dr/dθ)=−(1/θ^2 ) (√(r^2 +((dr/dθ))^2 ))=(√((1/θ^2 )+(1/θ^4 )))=((√(1+θ^2 ))/θ^2 ) L=∫_θ_1 ^θ_2 (√(r^2 +((dr/dθ))^2 ))dθ=∫_θ_1 ^θ_2 ((√(1+θ^2 ))/θ^2 )dθ [−((√(1+θ^2 ))/θ)+ln (θ+(√(1+θ^2 )))]_θ_1 ^θ_2 =[((√(1+θ_1 ^2 ))/θ_1 )−((√(1+θ_2 ^2 ))/θ_2 )+ln (((ϑ_2 +(√(1+θ_2 ^2 )))/(θ_1 +(√(1+θ_1 ^2 )))))] with θ_1 =3π^(−1) and θ_2 =nπ^(−1) line y=3π^(−1) : ⇒x=y×cot θ=3π^(−1) cot θ x_1 =3π^(−1) cot θ_1 x_2 =3π^(−1) cot θ_2 L_1 =∣∫_x_1 ^x_2 (√(1+(y′)^2 ))dx∣=∣∫_x_1 ^x_2 dx∣=x_1 −x_2 =3π^(−1) (cot θ_1 −cot θ_2 ) =3π^(−1) [cot (3π^(−1) )−cot (nπ^(−1) )] L≠L_1](Q11448.png)
Commented by mrW1 last updated on 26/Mar/17

Commented by ajfour last updated on 26/Mar/17
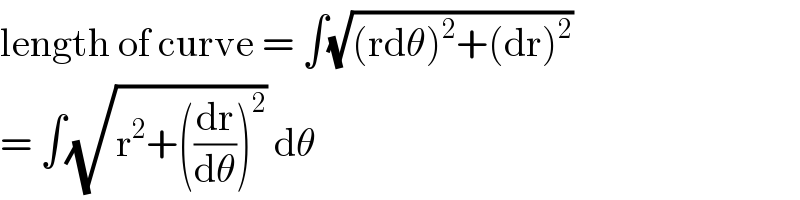
Commented by mrW1 last updated on 26/Mar/17

Commented by mrW1 last updated on 26/Mar/17

Commented by ajfour last updated on 26/Mar/17
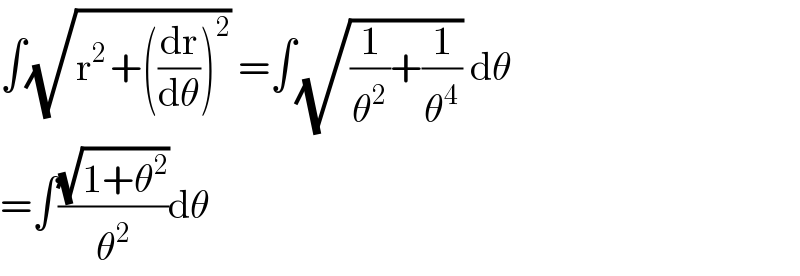
Commented by ajfour last updated on 26/Mar/17