
Question and Answers Forum
Question Number 75950 by turbo msup by abdo last updated on 21/Dec/19
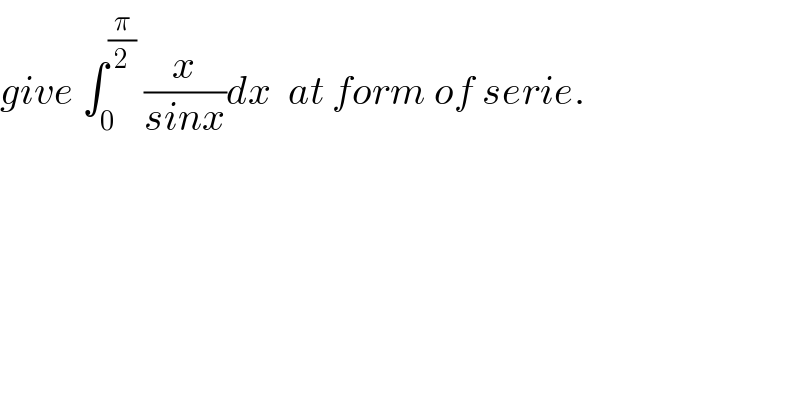
Commented by mathmax by abdo last updated on 22/Dec/19
![let A = ∫_0 ^(π/2) (x/(sinx))dx changement tan((x/2))=t give A =2∫_0 ^1 ((arctan(t))/((2t)/(1+t^2 )))((2dt)/(1+t^2 )) =2 ∫_0 ^1 ((arctan(t))/t)dt we have (d/dt)(arctant) =(1/(1+t^2 )) =Σ_(n=0) ^∞ (−1)^n t^(2n) ⇒ arctan(t) =Σ_(n=0) ^∞ (−1)^n (t^(2n+1) /(2n+1)) +c (c=0) ⇒ ((arctan(t))/t) =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))t^(2n) ⇒∫_0 ^1 ((arctan(t))/t)dt=Σ_(n=0) ^∞ (((−1)^n )/((2n+1)))∫_0 ^1 t^(2n) dt =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)))[(1/(2n+1))t^(2n+1) ]_0 ^1 =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) ⇒ A =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))](Q76046.png)
Commented by mathmax by abdo last updated on 22/Dec/19
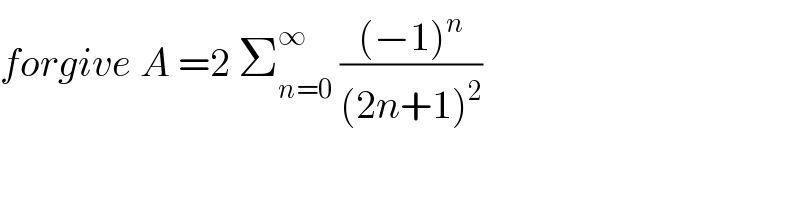
| ||
Question and Answers Forum | ||
Question Number 75950 by turbo msup by abdo last updated on 21/Dec/19 | ||
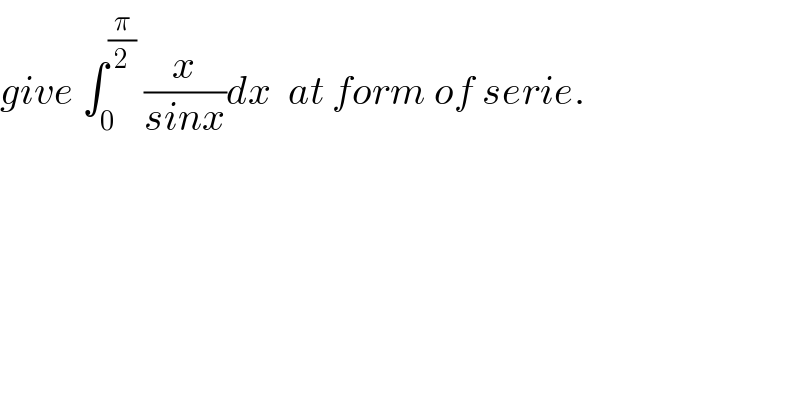 | ||
Commented by mathmax by abdo last updated on 22/Dec/19 | ||
![let A = ∫_0 ^(π/2) (x/(sinx))dx changement tan((x/2))=t give A =2∫_0 ^1 ((arctan(t))/((2t)/(1+t^2 )))((2dt)/(1+t^2 )) =2 ∫_0 ^1 ((arctan(t))/t)dt we have (d/dt)(arctant) =(1/(1+t^2 )) =Σ_(n=0) ^∞ (−1)^n t^(2n) ⇒ arctan(t) =Σ_(n=0) ^∞ (−1)^n (t^(2n+1) /(2n+1)) +c (c=0) ⇒ ((arctan(t))/t) =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))t^(2n) ⇒∫_0 ^1 ((arctan(t))/t)dt=Σ_(n=0) ^∞ (((−1)^n )/((2n+1)))∫_0 ^1 t^(2n) dt =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)))[(1/(2n+1))t^(2n+1) ]_0 ^1 =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) ⇒ A =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))](Q76046.png) | ||
Commented by mathmax by abdo last updated on 22/Dec/19 | ||
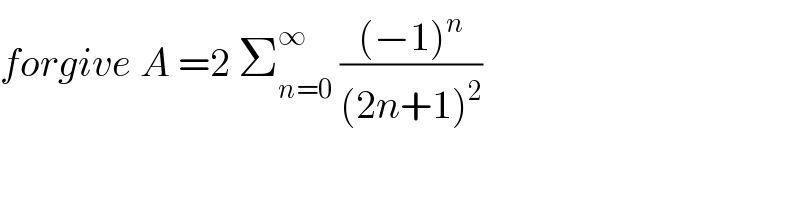 | ||