
Question and Answers Forum
Question Number 26757 by abdo imad last updated on 28/Dec/17
![give the decomposition of F(x) = (1/(x^(2n) +1)) inside C[x] then find the value of ∫_0 ^∞ (dx/(1+x^(2n) )) n∈N and n≠o](Q26757.png)
Commented by abdo imad last updated on 03/Jan/18
![let find the poles of F z^(2n) +1=0 ⇔ z^(2n) = e^(i(2k+1)π) so the poles of F are z_k = e^(i(((2k+1)π)/(2n))) k∈[[0,2n−1]] F(x)= Σ_(k=0) ^(2n−1) (λ_k /(x−z_k )) and λ_k = (1/(2n z_k ^(2n−1) )) =−(1/(2n)) z_k F(x)= −(1/(2n)) Σ_(k=0) ^(2n−1) (z_k /(x−z_k )) but z_0 = e^(i(π/(2n))) z_0 ^− = e^(−i(π/(2n ))) = e^(i(((2π−(π/(2n))))/)) = z_(2n−1) , z_1 ^− =z_(2n−2) ..... ⇒ F(x) =Σ_(k=0) ^(n−1) ( (z_k /(x−z_k )) + (z_k ^− /(x−z_k ^− )) ) .](Q27218.png)
Commented by abdo imad last updated on 03/Jan/18
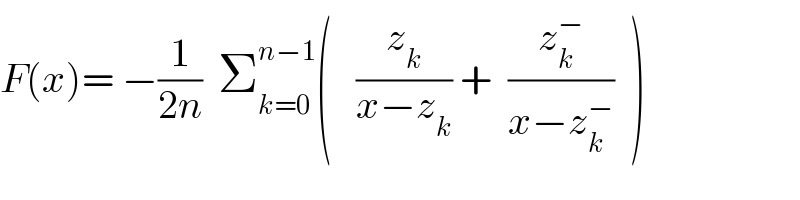
Commented by abdo imad last updated on 23/Jan/18

| ||
Question and Answers Forum | ||
Question Number 26757 by abdo imad last updated on 28/Dec/17 | ||
![give the decomposition of F(x) = (1/(x^(2n) +1)) inside C[x] then find the value of ∫_0 ^∞ (dx/(1+x^(2n) )) n∈N and n≠o](Q26757.png) | ||
Commented by abdo imad last updated on 03/Jan/18 | ||
![let find the poles of F z^(2n) +1=0 ⇔ z^(2n) = e^(i(2k+1)π) so the poles of F are z_k = e^(i(((2k+1)π)/(2n))) k∈[[0,2n−1]] F(x)= Σ_(k=0) ^(2n−1) (λ_k /(x−z_k )) and λ_k = (1/(2n z_k ^(2n−1) )) =−(1/(2n)) z_k F(x)= −(1/(2n)) Σ_(k=0) ^(2n−1) (z_k /(x−z_k )) but z_0 = e^(i(π/(2n))) z_0 ^− = e^(−i(π/(2n ))) = e^(i(((2π−(π/(2n))))/)) = z_(2n−1) , z_1 ^− =z_(2n−2) ..... ⇒ F(x) =Σ_(k=0) ^(n−1) ( (z_k /(x−z_k )) + (z_k ^− /(x−z_k ^− )) ) .](Q27218.png) | ||
Commented by abdo imad last updated on 03/Jan/18 | ||
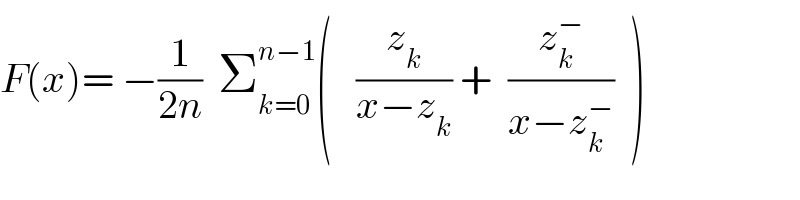 | ||
Commented by abdo imad last updated on 23/Jan/18 | ||
 | ||