Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 168225 by henderson last updated on 06/Apr/22

$$\mathrm{hi}!$$$$x\in ]\frac{\pi }{4};\frac{\pi }{3}[$$$$f\left(x\right)=\frac{1}{cosx}$$$$\mathrm{primitive}\mathrm{of}f\left(x\right).$$

Answered by MJS_new last updated on 06/Apr/22

$$\underset{\pi /4}{\stackrel{\pi /3}{\int }}\frac{dx}{\cos x}=$$$$[t=\tan \frac{x}{2}\to dx=\frac{2dt}{t^2+1}]$$$$=-2\underset{-1+\sqrt{2}}{\stackrel{1/\sqrt{3}}{\int }}\frac{dt}{t^2-1}=\int (\frac{1}{t+1}-\frac{1}{t+1})dt=$$$$={[\ln \mid t+1\mid -\ln \mid t-1\mid ]}_{-1+\sqrt{2}}^{1/\sqrt{3}}=$$$$=\ln (2+\sqrt{3})-\ln (1+\sqrt{2})$$$$$$$$\int \frac{dx}{\cos x}=\ln \mid \tan (\frac{x}{2}+\frac{\pi }{4})\mid +C=$$$$=\ln \mid \frac{\cos x}{1-\sin x}\mid +C$$

Answered by floor(10²Eta[1]) last updated on 06/Apr/22

$${\int }_{\pi /4}^{\pi /3}\frac{1}{\mathrm{cosx}}\mathrm{dx}={\int }_{\pi /4}^{\pi /3}\frac{\mathrm{cosx}}{{\cos }^2\mathrm{x}}\mathrm{dx}={\int }_{\pi /4}^{\pi /3}\frac{\mathrm{cosx}}{1-{\sin }^2\mathrm{x}}\mathrm{dx}$$$$\mathrm{u}=\mathrm{sinx}\Rightarrow \mathrm{du}=\mathrm{cosxdx}$$$${\int }_{\sqrt{2}/2}^{\sqrt{3}/2}\frac{\mathrm{du}}{1-{\mathrm{u}}^2}=\frac{1}{2}{\int }_{\sqrt{2}/2}^{\sqrt{3}/2}(\frac{1}{1-\mathrm{u}}+\frac{1}{1+\mathrm{u}})\mathrm{du}$$$$=-\frac{1}{2}{[\ln \mid 1-\mathrm{u}\mid ]}_{\sqrt{2}/2}^{\sqrt{3}/2}+\frac{1}{2}{[\ln \mid 1+\mathrm{u}\mid ]}_{\sqrt{2}/2}^{\sqrt{3}/2}$$$$-\frac{1}{2}(\ln (1-\frac{\sqrt{3}}{2})-\ln (1-\frac{\sqrt{2}}{2}))+\frac{1}{2}(\ln (1+\frac{\sqrt{3}}{2})-\ln (1+\frac{\sqrt{2}}{2}))$$$$=-\frac{1}{2}\ln \left(\frac{2-\sqrt{3}}{2}\right)+\frac{1}{2}\ln \left(\frac{2-\sqrt{2}}{2}\right)+\frac{1}{2}\ln \left(\frac{2+\sqrt{3}}{2}\right)-\frac{1}{2}\ln \left(\frac{2+\sqrt{2}}{2}\right)$$$$=\frac{1}{2}\ln \left(\frac{2+\sqrt{3}}{2-\sqrt{3}}\right)-\frac{1}{2}\ln \left(\frac{2+\sqrt{2}}{2-\sqrt{2}}\right)$$$$=\ln (2+\sqrt{3})-\ln (2+\sqrt{2})+\ln \sqrt{2}$$$$=\ln \left(\frac{2+\sqrt{3}}{\sqrt{2}+1}\right)$$$$$$$$$$

Commented by floor(10²Eta[1]) last updated on 06/Apr/22

$$\mathrm{thanks}\mathrm{i}\mathrm{corrected}\mathrm{it}$$

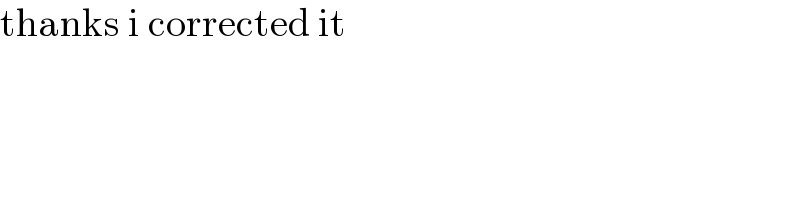
Commented by MJS_new last updated on 06/Apr/22

$$\mathrm{something}\mathrm{went}\mathrm{wrong}\mathrm{in}\mathrm{the}\mathrm{last}\mathrm{part}\mathrm{after}$$$$\mathrm{inserting}\mathrm{the}\mathrm{values}.\mathrm{the}\mathrm{integral}\mathrm{solution}\mathrm{is}$$$$\mathrm{ok}\mathrm{but}\mathrm{the}\mathrm{result}\mathrm{must}\mathrm{be}$$$$\ln \left((2+\sqrt{3})(-1+\sqrt{2})\right)=\ln (2+\sqrt{3})-\ln (1+\sqrt{2})$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com