
Question and Answers Forum
Question Number 100216 by Rio Michael last updated on 25/Jun/20
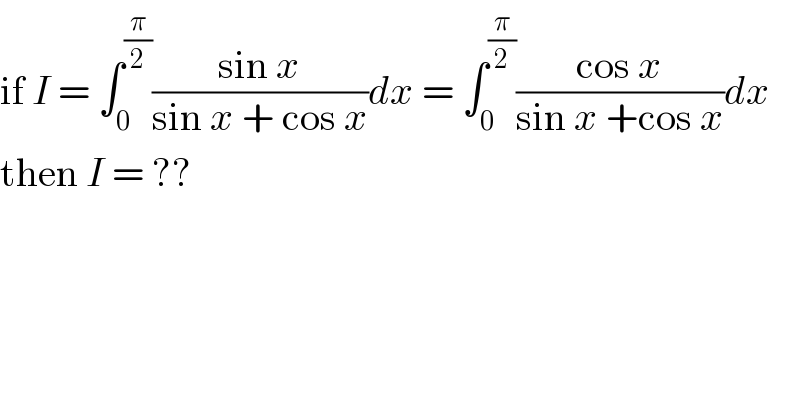
Commented by Dwaipayan Shikari last updated on 25/Jun/20
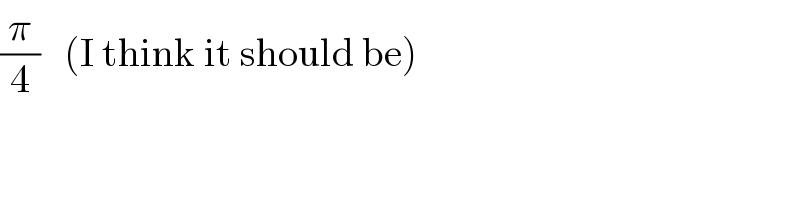
Commented by Dwaipayan Shikari last updated on 25/Jun/20
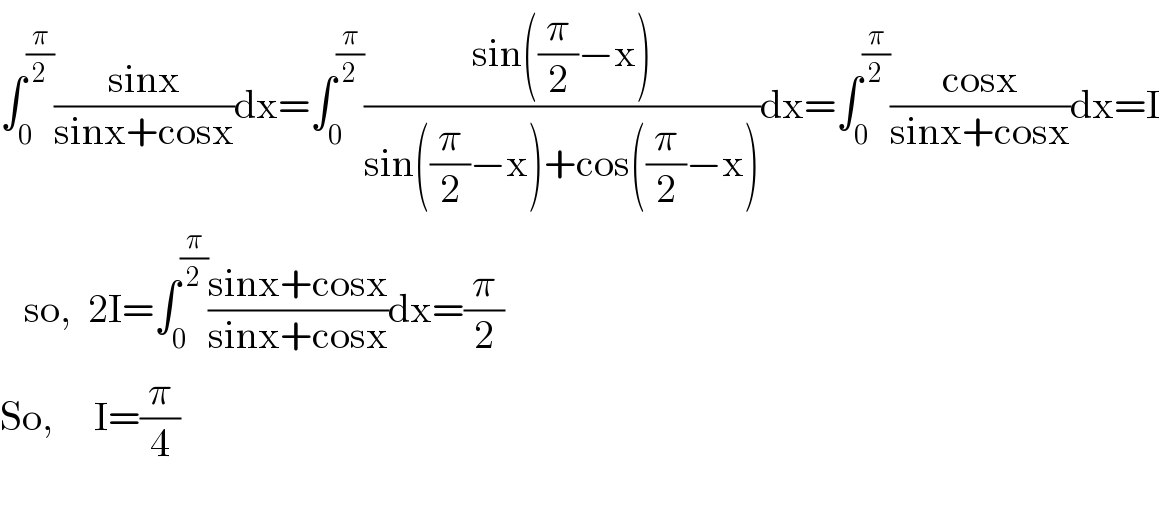
Answered by Ar Brandon last updated on 25/Jun/20
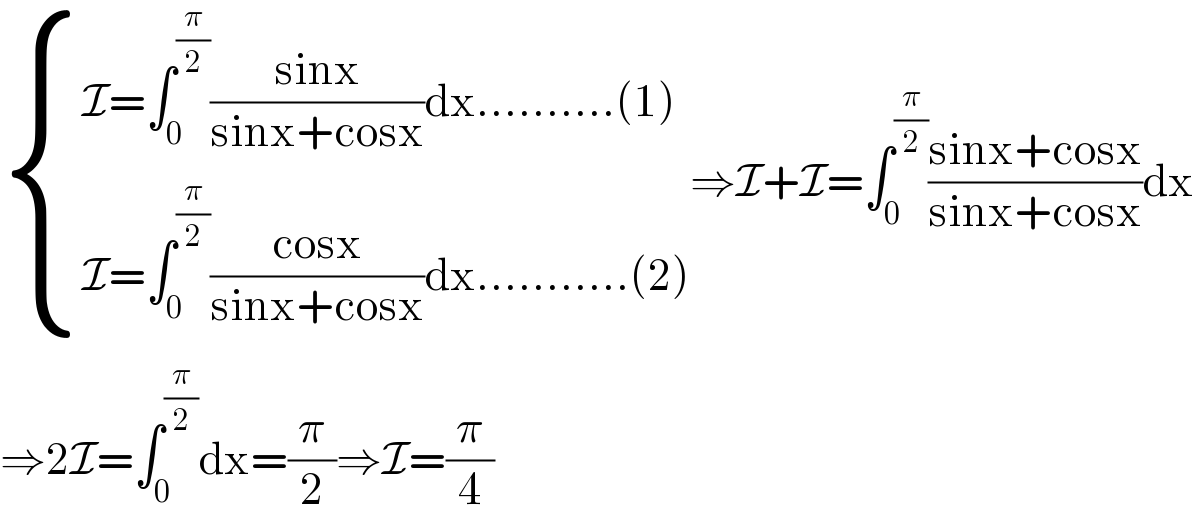
Commented by Coronavirus last updated on 25/Jun/20

Commented by Ar Brandon last updated on 25/Jun/20
Ouais
Commented by Rio Michael last updated on 26/Jun/20

