if a+b+c+d+e=8 and a^2 +b^2 +c^2 +d^2 +e^2 =16, what is the maximal value of a ?


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 180641 by mr W last updated on 14/Nov/22

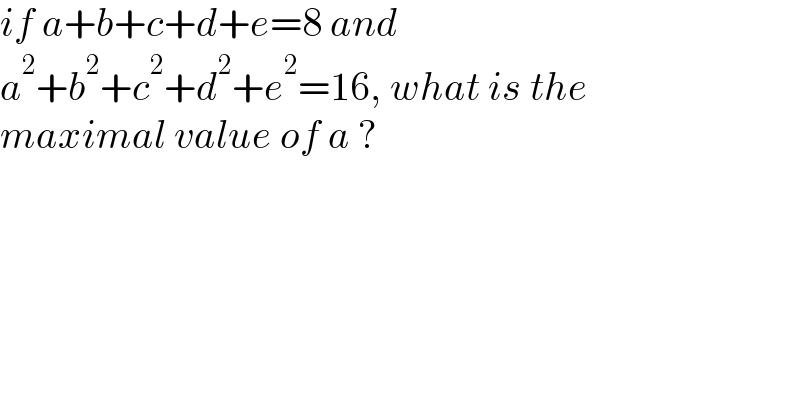
$i f a + b + c + d + e = 8 a n d$ $a^{2} + b^{2} + c^{2} + d^{2} + e^{2} = 16, w h a t i s t h e$ $m a x i m a l v a l u e o f a ?$
	Answered by Emrice last updated on 14/Nov/22

	$a < 4$
	Commented by Rasheed.Sindhi last updated on 15/Nov/22

	$a ⩽ 4$
	Commented by mr W last updated on 15/Nov/22

	$i f a = 4, t h e n b = c = d = e = 0, a n d$ $a + b + c + d + e = 4 \neq 8, t h e r e f o r e a m u s t$ $b e l e s s t h a n 4 .$
	Commented by Rasheed.Sindhi last updated on 15/Nov/22

	$Y e s s i r I u n d e r s t o o d .$
	Answered by a.lgnaoui last updated on 15/Nov/22

	$4$
	Answered by manxsol last updated on 15/Nov/22

	$s i a = 4$ $f_{1} 4 + . . . . . . . = 8 Σ (b + c + d + e) = 4$ $f_{2} > 16$ $a \neq 4$
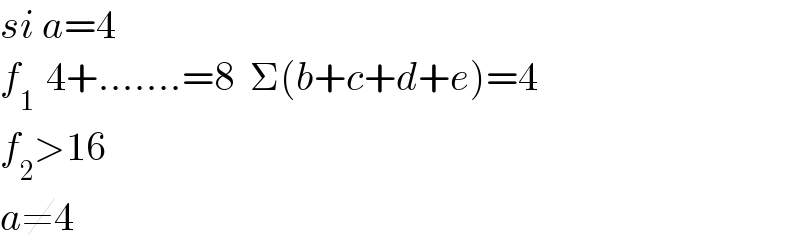
	Commented by manxsol last updated on 15/Nov/22

	$s i a = 4$ $f_{1} 4 + . . . . . . . = 8 Σ (b + c + d + e) = 4$ $f_{2} > 16$ $a \neq 4$ $\begin{array}{ccc} a & b & c & d & e \\ 3 & 2 & 1 & 1 & 1 & 8 \\ 9 & 4 & 1 & 1 & 1 & 16 \end{array}$
	Commented by mr W last updated on 15/Nov/22

	$a \neq 4, {t h a t}^{'} s t r u e . b u t a < 4 {d o e s n}^{'} t$ $m e a n t h e n e x t v a l u e f o r a i s 3, b e c a u s e$ $a, b, c, d, e {m u s n}^{'} t b e i n t e g e r .$
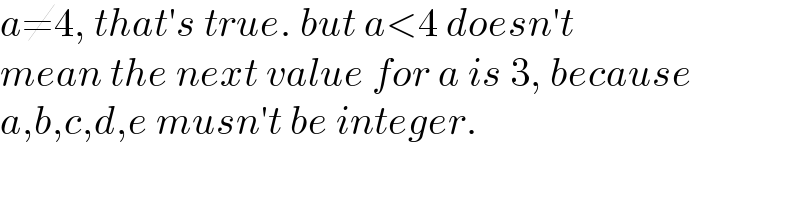
	Answered by mr W last updated on 15/Nov/22

	$t o g e t a a s l a r g e a s p o s s i b l e, t h e o t h e r$ $4 n u m b e r s s h o u l d b e a s c l o s e t o e a c h$ $o t h e r a s p o s s i b l e . t h a t m e a n s t h e$ $o t h e r n u m b e r s s h o u l d b e e q u a l, s a y$ $e q u a l t o x . t h e n w e h a v e$ $a + 4 x = 8$ $a^{2} + 4 x^{2} = 16$ $\Rightarrow 4 a^{2} + {(8 - a)}^{2} = 64$ $5 a^{2} - 16 a = 0$ $\Rightarrow a = \frac{16}{5} = 3.2$ $\Rightarrow x = \frac{6}{5} = 1.2$ $t h a t m e a n s w e g e t a_{m a x} = 3.2$ $w h e n b = c = d = e = 1.2 .$
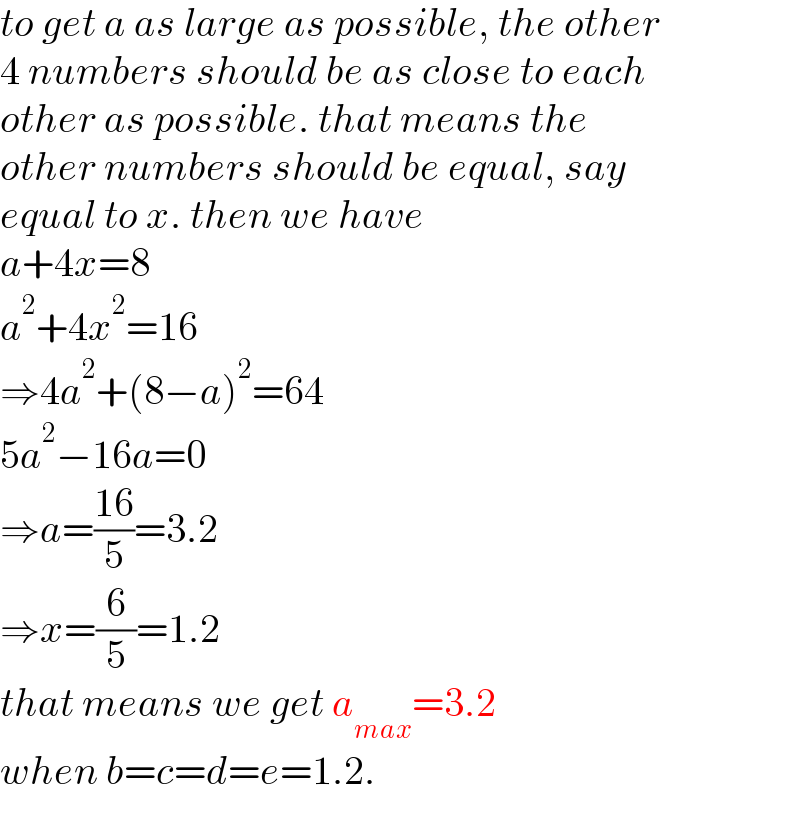
	Commented by manxsol last updated on 15/Nov/22
	Thanks Mr.W. I am learn.
	Commented by mr W last updated on 15/Nov/22

	$a n o t h e r m e t h o d$ $(l i t t l e t h i n k i n g, j u s t a p p l y i n g f o r m u l a)$ $a = 8 - (b + c + d + e)$ ${(8 - b - c - d - e)}^{2} + b^{2} + c^{2} + d^{2} + e^{2} - 16 = 0$ $Φ = 8 - (b + c + d + e) + λ [{(8 - b - c - d - e)}^{2} + b^{2} + c^{2} + d^{2} + e^{2} - 16]$ $\frac{\partial Φ}{\partial b} = - 1 + λ [- 2 (8 - b - c - d - e) + 2 b] = 0$ $\Rightarrow b = \frac{1}{2 λ} + 8 - (b + c + d + e)$ $s i m i l a r l y$ $\Rightarrow c = \frac{1}{2 λ} + 8 - (b + c + d + e)$ $\Rightarrow d = \frac{1}{2 λ} + 8 - (b + c + d + e)$ $\Rightarrow e = \frac{1}{2 λ} + 8 - (b + c + d + e)$ $\Rightarrow b = c = d = e = x, s a y$ $\frac{\partial Φ}{\partial λ} = {(8 - b - c - d - e)}^{2} + b^{2} + c^{2} + d^{2} + e^{2} - 16 = 0$ $\Rightarrow {(8 - 4 x)}^{2} + 4 x^{2} - 16 = 0$ $5 x^{2} - 16 x + 12 = 0$ $\Rightarrow x = \frac{8 \pm 2}{5} = 2 o r \frac{6}{5}$ $\Rightarrow a = 0 (m i n) o r \frac{16}{5} (m a x)$
	Commented by mr W last updated on 16/Nov/22

	$U s i n g L a g r a n g e M u l t i p l i e r m e t h o d$ $f o r f i n d i n g l o c a l m a x i m u m o r$ $m i n i m u m o f a f u n c t i o n w i t h m o r e$ $t h a n o n e v a r i a b l e u n d e r a c o n s t r a i n t .$
	Commented by manolex last updated on 16/Nov/22

	$w h a t t e o r y f o r m a t i o n Φ ?$
	Commented by mr W last updated on 16/Nov/22
	https://www.wikihow.com/Use-Lagrange-Multipliers
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum