
Question and Answers Forum
Question Number 53378 by Necxx last updated on 21/Jan/19
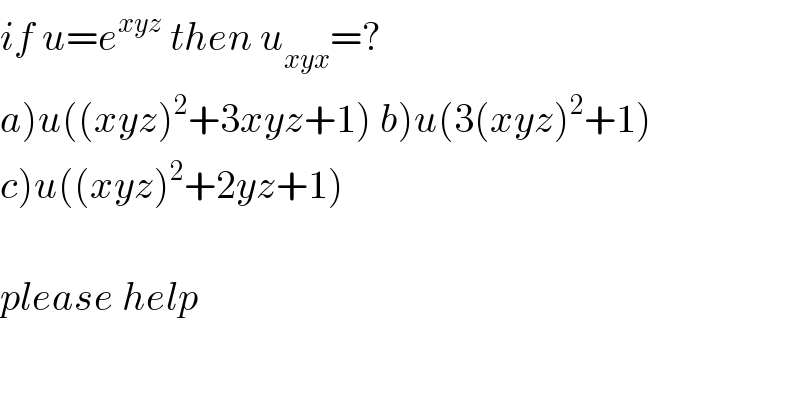
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19
![u=e^(xyz) u_x =e^(xyz) ×(∂/∂x)(xyz)=yze^(xyx) u_(xy) =(∂/∂y)(yze^(xyz) )=e^(xyz) ×z(∂/∂y)(y)+yz×(∂/∂y)(e^(xyz) ) =ze^(xyz) +yz×e^(xyz) ×xz =e^(xyz) (z+xyz^2 ) u_(xyz) =e^(xyz) ×(∂/∂z)(z+xyz^2 )+(z+xyz^2 )×(∂/∂z)(e^(xyz) ) =e^(xyz) ×(1+2xyz)+(z+xyz^2 )×e^(xyz) (xy) =u[1+2xyz+xyz+x^2 y^2 z^2 ] =u[1+3xyz+x^2 y^2 z^2 ] so option a is correct](Q53387.png)
Commented by Necxx last updated on 21/Jan/19

| ||
Question and Answers Forum | ||
Question Number 53378 by Necxx last updated on 21/Jan/19 | ||
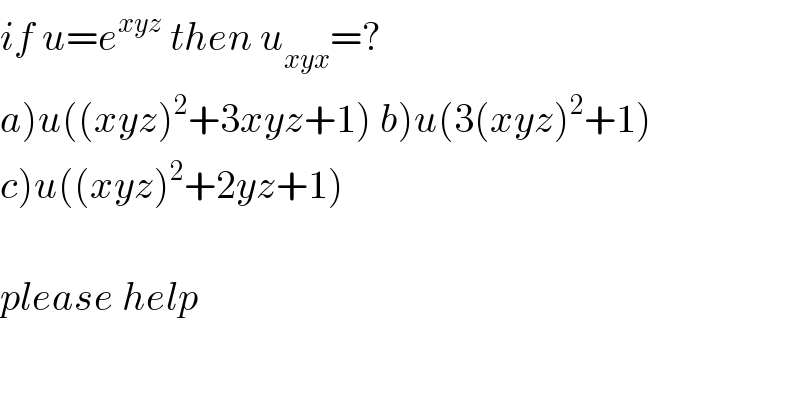 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19 | ||
![u=e^(xyz) u_x =e^(xyz) ×(∂/∂x)(xyz)=yze^(xyx) u_(xy) =(∂/∂y)(yze^(xyz) )=e^(xyz) ×z(∂/∂y)(y)+yz×(∂/∂y)(e^(xyz) ) =ze^(xyz) +yz×e^(xyz) ×xz =e^(xyz) (z+xyz^2 ) u_(xyz) =e^(xyz) ×(∂/∂z)(z+xyz^2 )+(z+xyz^2 )×(∂/∂z)(e^(xyz) ) =e^(xyz) ×(1+2xyz)+(z+xyz^2 )×e^(xyz) (xy) =u[1+2xyz+xyz+x^2 y^2 z^2 ] =u[1+3xyz+x^2 y^2 z^2 ] so option a is correct](Q53387.png) | ||
| ||
Commented by Necxx last updated on 21/Jan/19 | ||
 | ||