Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 151181 by mathdanisur last updated on 18/Aug/21

$$\mathrm{if}\mid \mathbf{x}\mid <1$$$$\mathrm{find}\mathrm{x}-{4\mathrm{x}}^2+{9\mathrm{x}}^3-{16\mathrm{x}}^4+...$$

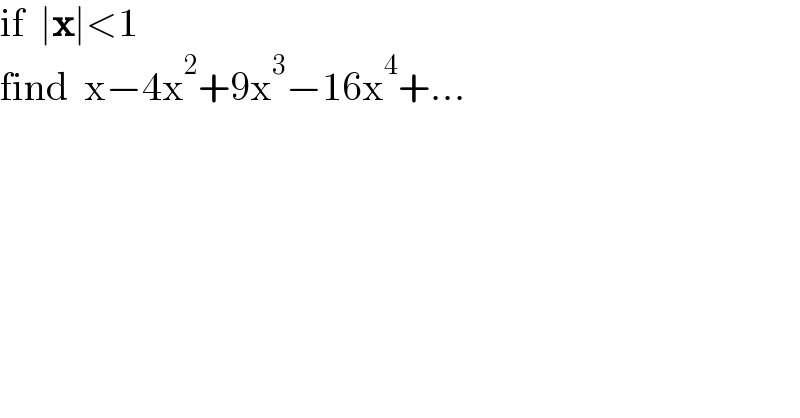
Answered by Olaf_Thorendsen last updated on 18/Aug/21

$$\mathrm{S}\left(x\right)=-\underset{n=1}{\sum ^{\mathrm{\infty }}}{(-1)}^n{n}^2{x}^n$$$$\mathrm{Let}f\left(x\right)=\frac{1}{1+x}=\underset{n=0}{\sum ^{\mathrm{\infty }}}{(-1)}^n{x}^n$$$$f^{\prime }\left(x\right)=-\frac{1}{{(1+x)}^2}=\underset{n=1}{\sum ^{\mathrm{\infty }}}{(-1)}^n{nx}^{n-1}$$$${xf}^{\prime }\left(x\right)=-\frac{x}{{(1+x)}^2}=\underset{n=1}{\sum ^{\mathrm{\infty }}}{(-1)}^n{nx}^n$$$$-\frac{1-x}{{(1+x)}^3}=\underset{n=1}{\sum ^{\mathrm{\infty }}}{(-1)}^n{n}^2{x}^{n-1}$$$$\frac{x(1-x)}{{(1+x)}^3}=-\underset{n=1}{\sum ^{\mathrm{\infty }}}{(-1)}^n{n}^2{x}^n=\mathrm{S}\left(x\right)$$

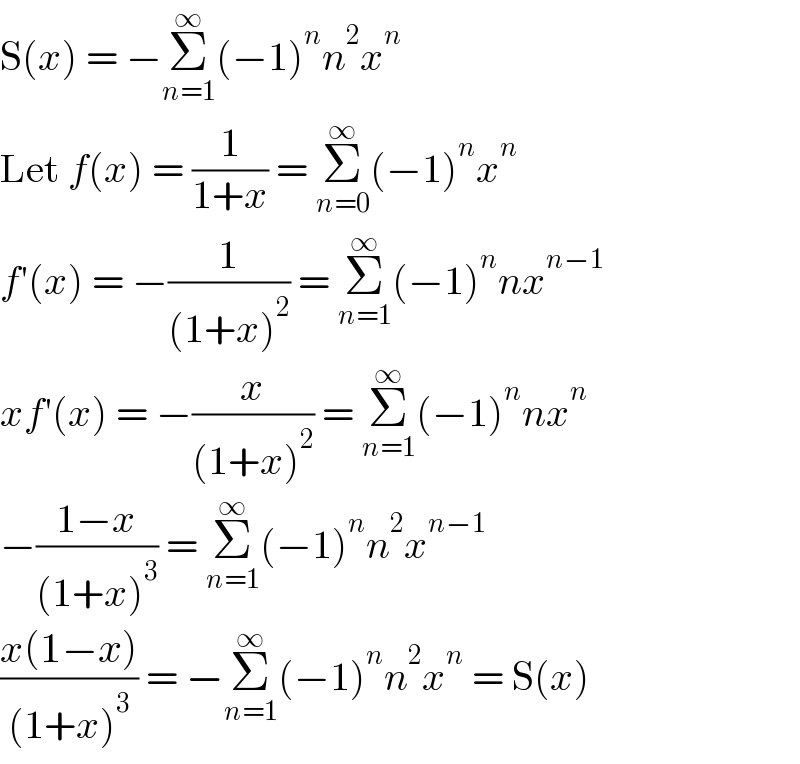
Commented by mathdanisur last updated on 18/Aug/21

$$\mathrm{Thank}\mathrm{you}\mathbf{S}\mathrm{er}$$

Commented by mathdanisur last updated on 19/Aug/21

$$\mathrm{Dear}\mathbf{S}\mathrm{er},\mathrm{finally}\mathrm{answer}\frac{\mathrm{x}(1-\mathrm{x})}{{(1+\mathrm{x})}^3}$$$$\mathrm{or}\frac{{2\mathrm{x}}^2}{{(1+\mathrm{x})}^3}.?$$

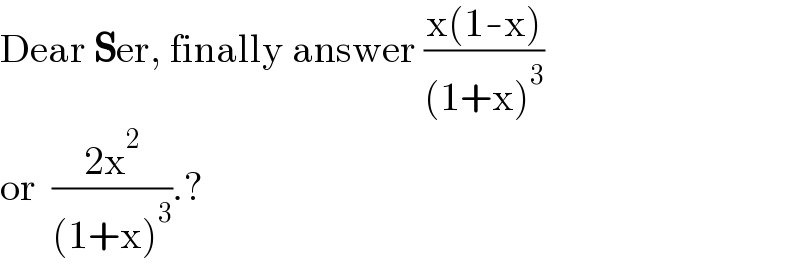
Answered by qaz last updated on 19/Aug/21

$$\underset{\mathrm{n}=1}{\sum ^{\mathrm{\infty }}}{\mathrm{n}}^2{(-1)}^{\mathrm{n}-1}{\mathrm{x}}^{\mathrm{n}}$$$$=\underset{\mathrm{n}=1}{\sum ^{\mathrm{\infty }}}(\mathrm{n}(\mathrm{n}+1)-\mathrm{n}){(-1)}^{\mathrm{n}-1}{\mathrm{x}}^{\mathrm{n}}$$$$=\underset{\mathrm{n}=1}{\sum ^{\mathrm{\infty }}}\mathrm{n}(\mathrm{n}+1){(-1)}^{\mathrm{n}-1}{\mathrm{x}}^{\mathrm{n}}-\underset{\mathrm{n}=1}{\sum ^{\mathrm{\infty }}}\mathrm{n}{(-1)}^{\mathrm{n}-1}{\mathrm{x}}^{\mathrm{n}}$$$$=2\underset{\mathrm{n}=1}{\sum ^{\mathrm{\infty }}}\underset{\mathrm{k}=1}{\sum ^{\mathrm{n}}}\mathrm{k}{(-1)}^{\mathrm{n}-1}{\mathrm{x}}^{\mathrm{n}}-\underset{\mathrm{n}=1}{\sum ^{\mathrm{\infty }}}\underset{\mathrm{k}=1}{\sum ^{\mathrm{n}}}{(-1)}^{\mathrm{n}-1}{\mathrm{x}}^{\mathrm{n}}$$$$=2\underset{\mathrm{k}=1}{\sum ^{\mathrm{\infty }}}\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\mathrm{k}{(-1)}^{\mathrm{n}+\mathrm{k}-1}{\mathrm{x}}^{\mathrm{n}+\mathrm{k}}-\underset{\mathrm{k}=1}{\sum ^{\mathrm{\infty }}}\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}{(-1)}^{\mathrm{n}+\mathrm{k}-1}{\mathrm{x}}^{\mathrm{n}+\mathrm{k}}$$$$=\frac{2}{1+\mathrm{x}}\underset{\mathrm{k}=0}{\sum ^{\mathrm{\infty }}}\underset{\mathrm{i}=0}{\sum ^{\mathrm{k}}}{(-1)}^{\mathrm{k}}{\mathrm{x}}^{\mathrm{k}+1}-\frac{\mathrm{x}}{{(1+\mathrm{x})}^2}$$$$=\frac{2}{1+\mathrm{x}}\underset{\mathrm{i}=0}{\sum ^{\mathrm{\infty }}}\underset{\mathrm{k}=0}{\sum ^{\mathrm{\infty }}}{(-1)}^{\mathrm{k}+\mathrm{i}}{\mathrm{x}}^{\mathrm{k}+\mathrm{i}+1}-\frac{\mathrm{x}}{{(1+\mathrm{x})}^2}$$$$=\frac{2\mathrm{x}}{{(1+\mathrm{x})}^3}-\frac{\mathrm{x}}{{(1+\mathrm{x})}^2}$$$$=\frac{\mathrm{x}-{\mathrm{x}}^2}{{(1+\mathrm{x})}^3}$$$$----------------$$$$\underset{\mathrm{n}=1}{\sum ^{\mathrm{\infty }}}{\mathrm{n}}^2{(-1)}^{\mathrm{n}-1}{\mathrm{x}}^{\mathrm{n}}$$$$=\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}({\mathrm{n}}^2+2\mathrm{n}+1){(-1)}^{\mathrm{n}}{\mathrm{x}}^{\mathrm{n}+1}$$$$=\mathrm{x}({\left(\mathrm{yD}\right)}^2+2\mathrm{yD}+1){\mid }_{\mathrm{y}=-\mathrm{x}}\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}{\mathrm{y}}^{\mathrm{n}}$$$$=\mathrm{x}({\mathrm{y}}^2{\mathrm{D}}^2+3\mathrm{yD}+1){\mid }_{\mathrm{y}=-\mathrm{x}}\frac{1}{1-\mathrm{y}}$$$$=\mathrm{x}{[\frac{{2\mathrm{y}}^2}{{(1-\mathrm{y})}^3}+\frac{3\mathrm{y}}{{(1-\mathrm{y})}^2}+\frac{1}{1-\mathrm{y}}]}_{\mathrm{y}=-\mathrm{x}}$$$$=\frac{\mathrm{x}(1-\mathrm{x})}{{(1+\mathrm{x})}^3}$$

Commented by mathdanisur last updated on 19/Aug/21

$$\mathrm{Thank}\mathrm{you}\mathbf{S}\mathrm{er}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com