
Question and Answers Forum
Question Number 105488 by 175mohamed last updated on 29/Jul/20
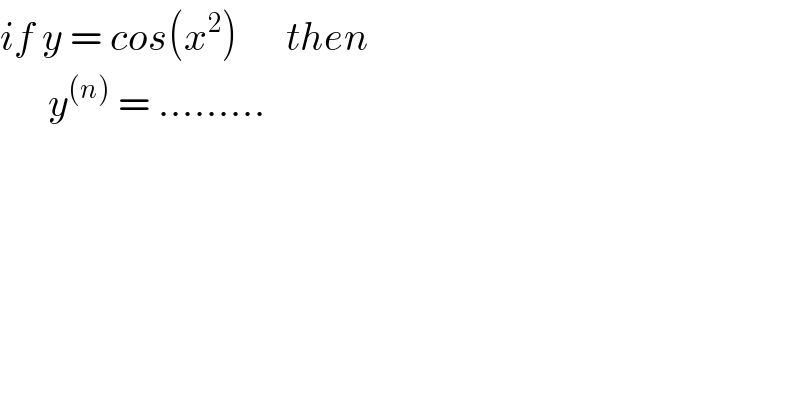
Answered by mathmax by abdo last updated on 29/Jul/20
![y(x) =cos(x^2 ) =((e^(ix^2 ) +e^(−ix^2 ) )/2) ⇒y^((n)) (x) =(1/2)(e^(ix^2 ) )^((n)) +(1/2)(e^(−ix^2 ) )^()n)) let w(x) =(e^(ix^2 ) ) we have w^((1)) (x) =2ix e^(ix^2 ) w^((2)) (x) =2i e^(ix^2 ) +2ix(2ix) e^(ix^2 ) =(−4x^2 +2i)e^(ix^2 ) ⇒ w^((n)) =p_n (x) e^(ix^2 ) with p_n ∈ C[x] we have w^((n+1)) (x) =p_n ^′ (x)e^(ix^2 ) +2ix p_n (x)e^(ix^2 ) =(2ip_n (x)+p_n ^′ (x))e^(ix^2 ) ⇒ ⇒p_(n+1) (x) =2ip_n (x)+p_n ^′ (x) let ϕ(x) =e^(−ix^2 ) ⇒ϕ^((1)) (x) =−2ix e^(−ix^2 ) and ϕ^((2)) (x) =−2i e^(−ix^2 ) +(−2ix)(−2ix) e^(−ix^2 ) =(−4x^2 −2i)e^(−ix^2 ) ⇒ ϕ^((n)) (x) =q_n (x)e^(−ix^2 ) (q_n ∈C [x]) we have ϕ^((n+1)) (x) =q_n ^′ (x)e^(−ix^2 ) −2ixq_n (x)e^(−ix^2 ) =(q_n ^′ (x)−2iq_n (x))e^(−ix^2 ) ⇒q_(n+1) =q_n ^(′ ) −2iq_n (x) and we get y^((n)) (x) =w^((n)) (x)+ϕ^((n)) (x)](Q105547.png)
| ||
Question and Answers Forum | ||
Question Number 105488 by 175mohamed last updated on 29/Jul/20 | ||
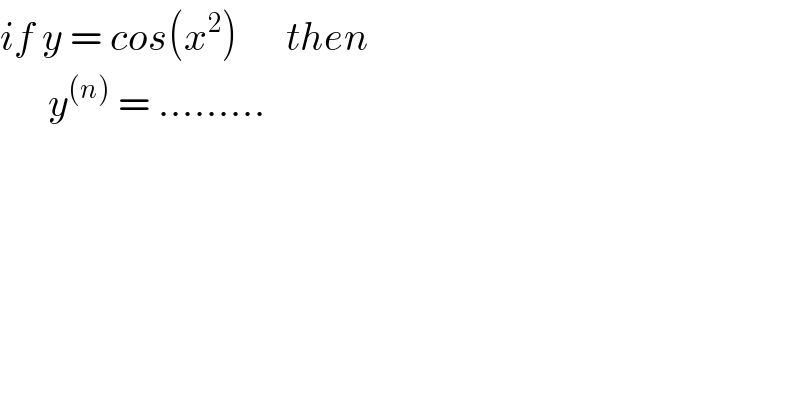 | ||
Answered by mathmax by abdo last updated on 29/Jul/20 | ||
![y(x) =cos(x^2 ) =((e^(ix^2 ) +e^(−ix^2 ) )/2) ⇒y^((n)) (x) =(1/2)(e^(ix^2 ) )^((n)) +(1/2)(e^(−ix^2 ) )^()n)) let w(x) =(e^(ix^2 ) ) we have w^((1)) (x) =2ix e^(ix^2 ) w^((2)) (x) =2i e^(ix^2 ) +2ix(2ix) e^(ix^2 ) =(−4x^2 +2i)e^(ix^2 ) ⇒ w^((n)) =p_n (x) e^(ix^2 ) with p_n ∈ C[x] we have w^((n+1)) (x) =p_n ^′ (x)e^(ix^2 ) +2ix p_n (x)e^(ix^2 ) =(2ip_n (x)+p_n ^′ (x))e^(ix^2 ) ⇒ ⇒p_(n+1) (x) =2ip_n (x)+p_n ^′ (x) let ϕ(x) =e^(−ix^2 ) ⇒ϕ^((1)) (x) =−2ix e^(−ix^2 ) and ϕ^((2)) (x) =−2i e^(−ix^2 ) +(−2ix)(−2ix) e^(−ix^2 ) =(−4x^2 −2i)e^(−ix^2 ) ⇒ ϕ^((n)) (x) =q_n (x)e^(−ix^2 ) (q_n ∈C [x]) we have ϕ^((n+1)) (x) =q_n ^′ (x)e^(−ix^2 ) −2ixq_n (x)e^(−ix^2 ) =(q_n ^′ (x)−2iq_n (x))e^(−ix^2 ) ⇒q_(n+1) =q_n ^(′ ) −2iq_n (x) and we get y^((n)) (x) =w^((n)) (x)+ϕ^((n)) (x)](Q105547.png) | ||
| ||