
Question and Answers Forum
Question Number 21810 by j.masanja06@gmail.com last updated on 04/Oct/17
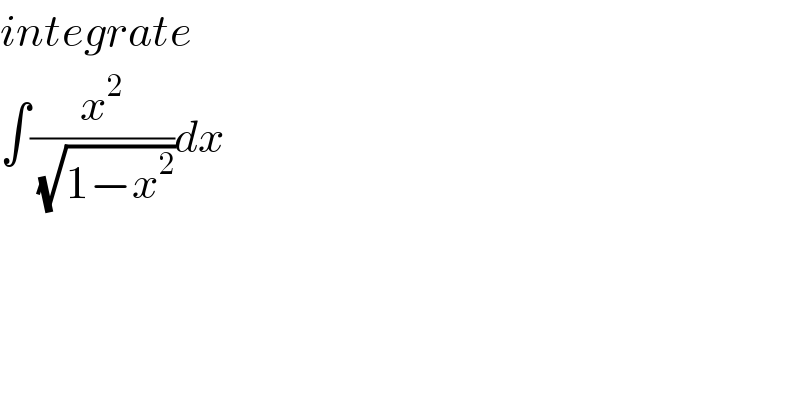
Answered by sma3l2996 last updated on 04/Oct/17
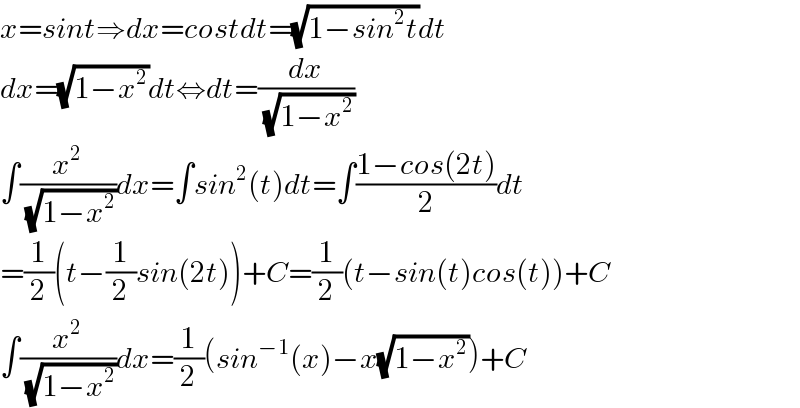
| ||
Question and Answers Forum | ||
Question Number 21810 by j.masanja06@gmail.com last updated on 04/Oct/17 | ||
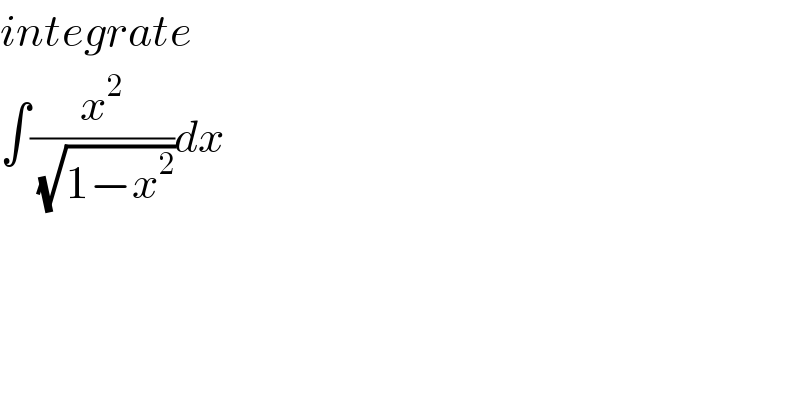 | ||
Answered by sma3l2996 last updated on 04/Oct/17 | ||
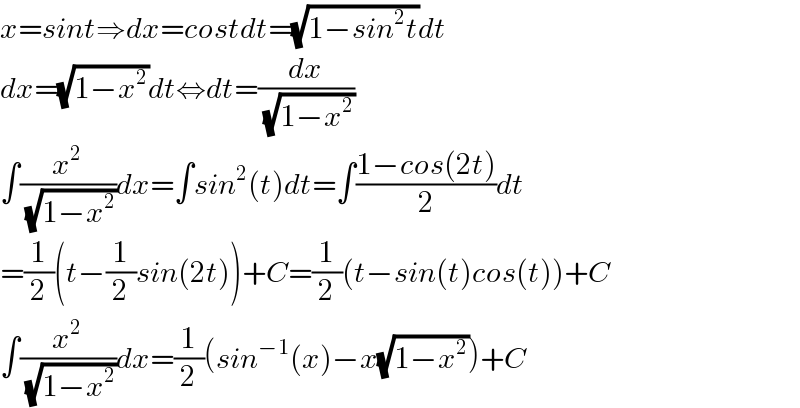 | ||
| ||