
Question and Answers Forum
Question Number 35049 by math khazana by abdo last updated on 14/May/18
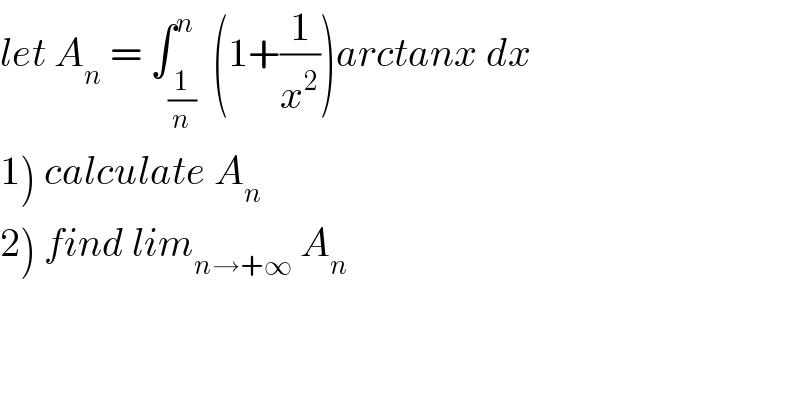
Commented by abdo mathsup 649 cc last updated on 16/May/18
![1) let integrate by parts u^′ =1+(1/x^2 ) and v=arctanx A_n = [(1−(1/x))arctanx]_(1/n) ^n −∫_(1/n) ^n (1−(1/x)) (dx/(1+x^2 )) =(1−(1/n))arctan(n) −(1−n)arctan((1/n)) − ∫_(1/n) ^n (dx/(1+x^2 )) + ∫_(1/n) ^n (dx/(x(1+x^2 ))) but ∫_(1/n) ^n (dx/(1+x^2 )) = arctan(n) −arctan((1/n)) ∫_(1/n) ^n (1/(x(1+x^2 ))) dx= ∫_(1/n) ^n ((1/x) −(x/(1+x^2 )))dx =ln(n) −ln((1/n)) −(1/2)[ln(1+x^2 )]_(1/n) ^n = 2ln(n) −(1/2){ ln(1+n^2 ) −ln(1+(1/n^2 ))}⇒ A_n = (1−(1/n))arctan(n)−(1−n)arctan((1/n)) −arctan(n) +arctan((1/n)) +2ln(n)−(1/2)(2ln(n)) A_n =−((arctan(n))/n) +n arctan((1/n)) +(π/2) −2arctan(n) +ln(n) 2) we have lim_(n→+∞) ( −((arctan(n))/n) +n arctan((1/n)) +(π/2) −2arctsn(n)) =0 +1 −(π/2) −π but lim_(n→+∞) ln(n) =+∞ ⇒ lim_(n→+∞) A_n = +∞.](Q35145.png)
Answered by MJS last updated on 15/May/18
![∫(1+(1/x^2 ))arctan(x)dx= =∫arctan(x)dx+∫((arctan(x))/x^2 )dx= ∫arctan(x)dx= [((∫u′v=uv−∫uv′)),((u′=1 ⇒ u=x)),((v=arctan(x) ⇒ v′=(1/(x^2 +1)))) ] =xarctan(x)−∫(x/(x^2 +1))dx= [((t=x^2 +1 → dx=(dt/(2x)))) ] =xarctan(x)−(1/2)∫(1/t)dt= =xarctan(x)−((ln(t))/2)= =xarctan(x)−((ln(x^2 +1))/2) ∫((arctan(x))/x^2 )dx= [((∫u′v=uv−∫uv′)),((u′=(1/x^2 ) ⇒ u=−(1/x))),((v=arctan(x) ⇒ v′=(1/(x^2 +1)))) ] =−((arctan(x))/x)+∫(1/(x(x^2 +1)))dx= =−((arctan(x))/x)+∫((1/x)−(x^2 /(x^2 +1)))dx= [((same as above)) ] =−((arctan(x))/x)+ln(x)−((ln(x^2 +1))/2) =xarctan(x)−((ln(x^2 +1))/2)−((arctan(x))/x)+ln(x)−((ln(x^2 +1))/2)= =(((x^2 −1)/x))arctan(x)+ln((x/(x^2 +1)))+C ∫_(1/n) ^n (1+(1/x^2 ))arctan(x)dx= =(((n^2 −1)/n))arctan(n)+ln((n/(n^2 +1)))−(((((1/n^2 )−1)/(1/n)))arctan((1/n))+ln(((1/n)/((1/n^2 )+1))))= =(((n^2 −1)/n))arctan(n)+ln((n/(n^2 +1)))−((((1−n^2 )/n))((π/2)−arctan(n))+ln((n/(n^2 +1))))= =((π(n^2 −1))/(2n)) lim_(n→∞) ((π(n^2 −1))/(2n))=(π/2)lim_(n→∞) (n−(1/n))=∞](Q35081.png)
| ||
Question and Answers Forum | ||
Question Number 35049 by math khazana by abdo last updated on 14/May/18 | ||
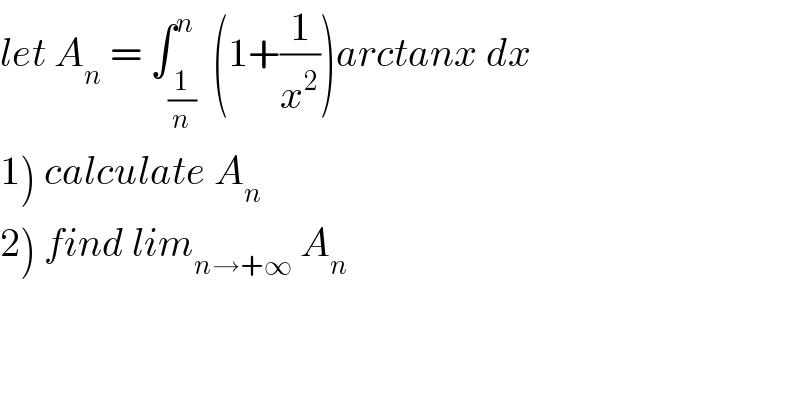 | ||
Commented by abdo mathsup 649 cc last updated on 16/May/18 | ||
![1) let integrate by parts u^′ =1+(1/x^2 ) and v=arctanx A_n = [(1−(1/x))arctanx]_(1/n) ^n −∫_(1/n) ^n (1−(1/x)) (dx/(1+x^2 )) =(1−(1/n))arctan(n) −(1−n)arctan((1/n)) − ∫_(1/n) ^n (dx/(1+x^2 )) + ∫_(1/n) ^n (dx/(x(1+x^2 ))) but ∫_(1/n) ^n (dx/(1+x^2 )) = arctan(n) −arctan((1/n)) ∫_(1/n) ^n (1/(x(1+x^2 ))) dx= ∫_(1/n) ^n ((1/x) −(x/(1+x^2 )))dx =ln(n) −ln((1/n)) −(1/2)[ln(1+x^2 )]_(1/n) ^n = 2ln(n) −(1/2){ ln(1+n^2 ) −ln(1+(1/n^2 ))}⇒ A_n = (1−(1/n))arctan(n)−(1−n)arctan((1/n)) −arctan(n) +arctan((1/n)) +2ln(n)−(1/2)(2ln(n)) A_n =−((arctan(n))/n) +n arctan((1/n)) +(π/2) −2arctan(n) +ln(n) 2) we have lim_(n→+∞) ( −((arctan(n))/n) +n arctan((1/n)) +(π/2) −2arctsn(n)) =0 +1 −(π/2) −π but lim_(n→+∞) ln(n) =+∞ ⇒ lim_(n→+∞) A_n = +∞.](Q35145.png) | ||
Answered by MJS last updated on 15/May/18 | ||
![∫(1+(1/x^2 ))arctan(x)dx= =∫arctan(x)dx+∫((arctan(x))/x^2 )dx= ∫arctan(x)dx= [((∫u′v=uv−∫uv′)),((u′=1 ⇒ u=x)),((v=arctan(x) ⇒ v′=(1/(x^2 +1)))) ] =xarctan(x)−∫(x/(x^2 +1))dx= [((t=x^2 +1 → dx=(dt/(2x)))) ] =xarctan(x)−(1/2)∫(1/t)dt= =xarctan(x)−((ln(t))/2)= =xarctan(x)−((ln(x^2 +1))/2) ∫((arctan(x))/x^2 )dx= [((∫u′v=uv−∫uv′)),((u′=(1/x^2 ) ⇒ u=−(1/x))),((v=arctan(x) ⇒ v′=(1/(x^2 +1)))) ] =−((arctan(x))/x)+∫(1/(x(x^2 +1)))dx= =−((arctan(x))/x)+∫((1/x)−(x^2 /(x^2 +1)))dx= [((same as above)) ] =−((arctan(x))/x)+ln(x)−((ln(x^2 +1))/2) =xarctan(x)−((ln(x^2 +1))/2)−((arctan(x))/x)+ln(x)−((ln(x^2 +1))/2)= =(((x^2 −1)/x))arctan(x)+ln((x/(x^2 +1)))+C ∫_(1/n) ^n (1+(1/x^2 ))arctan(x)dx= =(((n^2 −1)/n))arctan(n)+ln((n/(n^2 +1)))−(((((1/n^2 )−1)/(1/n)))arctan((1/n))+ln(((1/n)/((1/n^2 )+1))))= =(((n^2 −1)/n))arctan(n)+ln((n/(n^2 +1)))−((((1−n^2 )/n))((π/2)−arctan(n))+ln((n/(n^2 +1))))= =((π(n^2 −1))/(2n)) lim_(n→∞) ((π(n^2 −1))/(2n))=(π/2)lim_(n→∞) (n−(1/n))=∞](Q35081.png) | ||
| ||