
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 68019 by mathmax by abdo last updated on 03/Sep/19
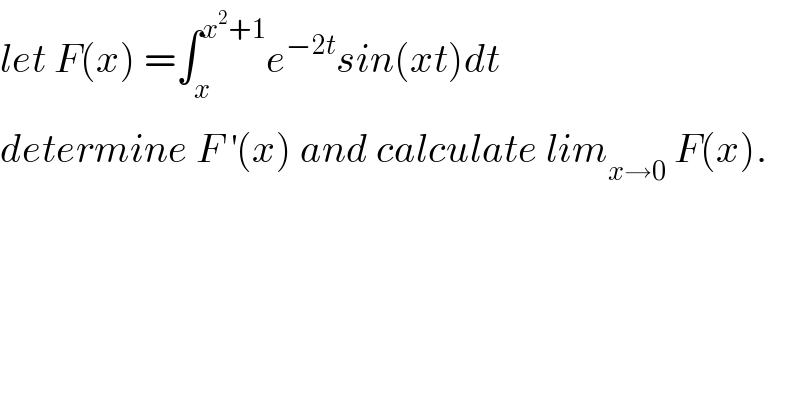
Commented by kaivan.ahmadi last updated on 05/Sep/19

Commented by mathmax by abdo last updated on 05/Sep/19
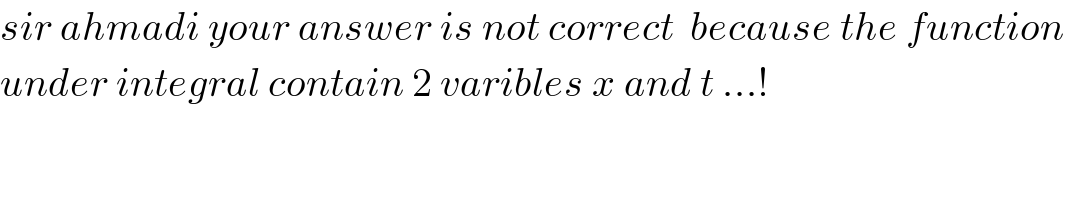
Commented by mathmax by abdo last updated on 05/Sep/19
![F(x) =∫_x ^(x^2 +1) e^(−2t) sin(xt)dt we have u(x)=x and v(x)=x^2 +1and g(x,t) =e^(−2t) sin(xt) we use the formulae F^, (x) =∫_(u(x)) ^(v(x)) (∂g/∂x)(x,t)dt +v^′ g(x,v)−u^′ g(x,u) =∫_x ^(x^2 +1) t e^(−2t) cos(xt)dt +2x g(x,x^2 +1)−g(x,x^2 ) =∫_x ^(x^2 +1) t e^(−2t) cos(xt)dt +2xe^(−2(x^2 +1)) sin(x(x^2 +1))−e^(−2x^2 ) sin(x^3 ) we have ∫_x ^(x^2 +1 ) t e^(−2t) cos(xt)dt =Re(∫_x ^(x^2 +1) t e^(−2t+ixt) dt) ∫_x ^(x^2 +1) t e^((−2+ix)t) dt =[(t/(−2+ix)) e^((−2+ix)t) ]_(t=x) ^(t=x^2 +1) −∫_x ^(x^2 +1) (1/(−2+ix))e^((−2+ix)t) dt =(1/(−2+ix)){(x^2 +1)e^((−2+ix)(x^2 +1)) −xe^((−2+ix)x) } −(1/(−2+ix)) ∫_x ^(x^2 +1) e^((−2+ix)t) dt ....rest to finich the calculus.](Q68103.png)
Commented by mathmax by abdo last updated on 06/Sep/19
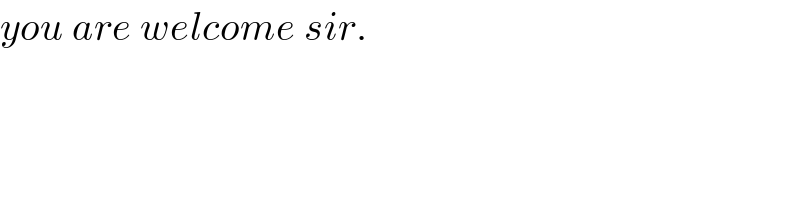
Commented by mathmax by abdo last updated on 08/Sep/19
![we have F(x)=∫_x ^(x^2 +1) e^(−2t) sin(xt)dt ⇒F(x)=Im(∫_x ^(x^2 +1) e^(−2t+ixt) dt) ∫_x ^(x^2 +1) e^((−2+ix)t) dt =[(1/(−2+ix)) e^((−2+ix)t) ]_x ^(x^2 +1) =((−1)/(2−ix)){ e^((−2+ix)(x^2 +1)) −e^((−2+ix)x) } =((−1)/(2−ix)){ e^(−2(x^2 +1)) e^(i(x^3 +x)) −e^(−2x) e^(ix^2 ) } =((−1)/(2−ix)){ e^(−2x^2 −2) (cos(x^3 +x)+isin(x^3 +x)−e^(−2x) (cos(x^2 )+isin(x^2 )} =−((2+ix)/(4+x^2 )){ e^(−2x^2 −2) cos(x^3 +x)−e^(−2x) cos(x^2 ) +i( e^(−2x^2 −2) sin(x^3 +x)−e^(−2x) sin(x^2 )} =−(1/(4+x^2 ))(2+ix){......} =−(1/(4+x^2 )){ 2( e^(−2x^2 −2) cos(x^3 +x)−e^(−2x) cos(x^2 )) +2i(e^(−2x^2 −2) sin(x^3 +x)−e^(−2x) sin(x^2 )) +ix( e^(−2x^2 −2) cos(x^3 +x) −e^(−2x) cos(x^2 )−x(e^(−2x^2 −2) sin(x^3 +x)−e^(−2x) sin(x^2 )} ⇒ F(x) =−(1/(4+x^2 )){ 2(e^(−2x^2 −2) sin(x^3 +x)−e^(−2x) sin(x^2 )) +x(e^(−2x^2 −2) cos(x^3 +x)−e^(−2x) cos(x^2 )} ⇒lim_(x→0) F(x) =0](Q68258.png)
