
Question and Answers Forum
Question Number 68879 by mathmax by abdo last updated on 16/Sep/19
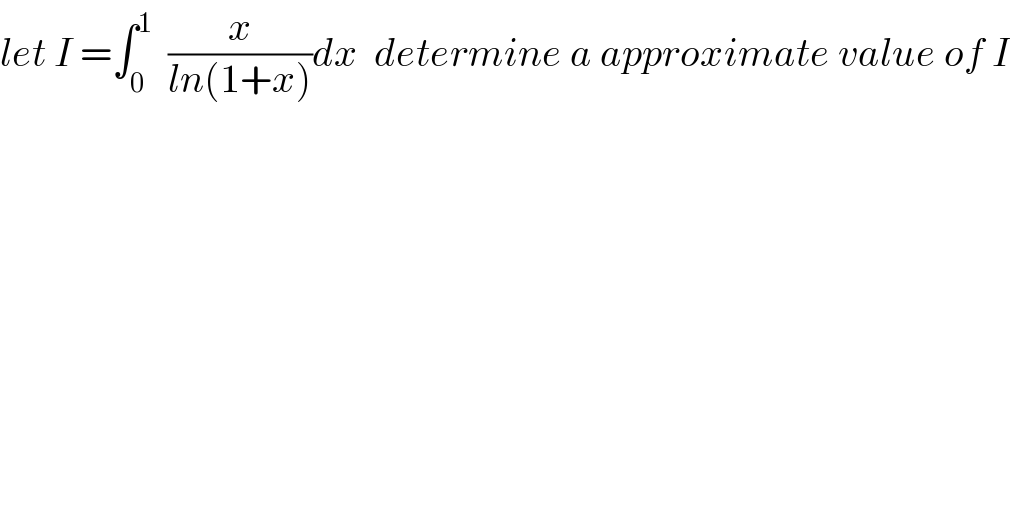
Commented by Abdo msup. last updated on 21/Sep/19

Commented by mathmax by abdo last updated on 22/Sep/19
![we have ln^′ (1+x) =(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ ln(1+x) =Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) +c (c=0) ⇒ ln(1+x) =x−(x^2 /2) +(x^3 /3) −... ⇒x−(x^2 /2) ≤ln(1+x) ≤x ⇒ (1/x) ≤(1/(ln(1+x))) ≤(1/(x−(x^2 /2))) ⇒ 1 ≤ (x/(ln(1+x))) ≤(1/(1−(x/2))) ⇒ 1≤ ∫_0 ^1 (x/(ln(1+x)))dx ≤∫_0 ^1 (dx/(1−(x/2))) we have ∫_0 ^1 (dx/(1−(x/2))) =∫_0 ^1 ((2dx)/(2−x)) =−2 ∫_0 ^1 (dx/(x−2)) =−2[ln∣x−2∣]_0 ^1 =−2(−ln2) =2ln(2) ⇒ 1 ≤I ≤2ln(2) so v_0 =((1+2ln(2))/2) is a approximate value of I .](Q69380.png)
| ||
Question and Answers Forum | ||
Question Number 68879 by mathmax by abdo last updated on 16/Sep/19 | ||
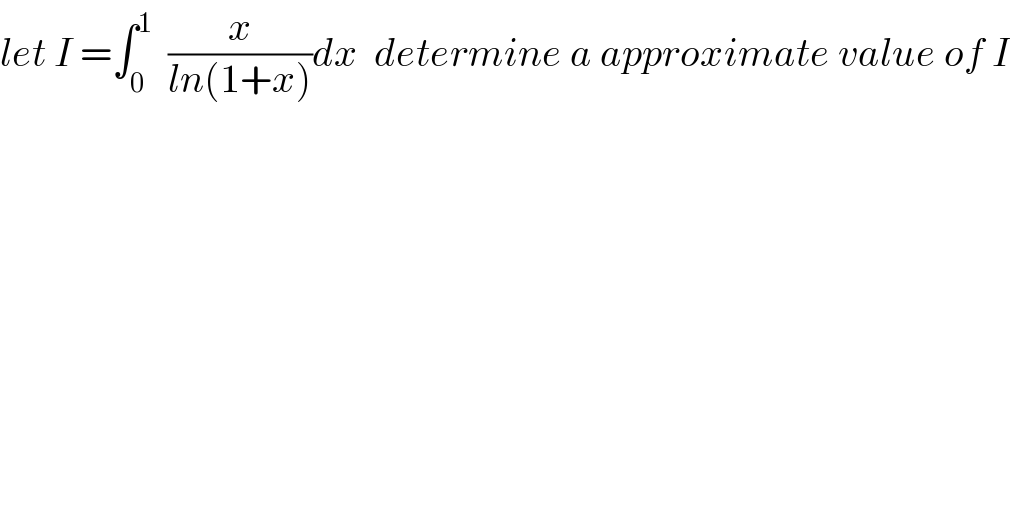 | ||
Commented by Abdo msup. last updated on 21/Sep/19 | ||
 | ||
Commented by mathmax by abdo last updated on 22/Sep/19 | ||
![we have ln^′ (1+x) =(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ ln(1+x) =Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) +c (c=0) ⇒ ln(1+x) =x−(x^2 /2) +(x^3 /3) −... ⇒x−(x^2 /2) ≤ln(1+x) ≤x ⇒ (1/x) ≤(1/(ln(1+x))) ≤(1/(x−(x^2 /2))) ⇒ 1 ≤ (x/(ln(1+x))) ≤(1/(1−(x/2))) ⇒ 1≤ ∫_0 ^1 (x/(ln(1+x)))dx ≤∫_0 ^1 (dx/(1−(x/2))) we have ∫_0 ^1 (dx/(1−(x/2))) =∫_0 ^1 ((2dx)/(2−x)) =−2 ∫_0 ^1 (dx/(x−2)) =−2[ln∣x−2∣]_0 ^1 =−2(−ln2) =2ln(2) ⇒ 1 ≤I ≤2ln(2) so v_0 =((1+2ln(2))/2) is a approximate value of I .](Q69380.png) | ||